Pythonによる時系列データ入門：グラフによる分析からモデル作成まで

この記事では、Pythonとstatsmodelsライブラリを使った時系列データの基本的な扱い方から、グラフ作成、予測モデルの構築に至るまでをステップバイステップで解説していきます。

時系列データとは？

時系列データとは、簡単に言えば「時間と共に記録されたデータ」です。これは、毎日の気温、毎月の店舗売上、毎分のインターネットトラフィックなど、あらゆるものが対象になります。私たちの周りには、時間とともに変わる多くの事象があり、それらをデータとして記録することで、過去の変化を見たり未来を予測したりする手がかりを得ることができます。

特にビジネスの世界では、「売上は冬に上がる」「夏にはアイスクリームがよく売れる」といった季節のパターンや、経年での売上の増減といったトレンドが重要です。これらは、時系列データが時間の経過とともにどのように変化するかを示すもので、この情報は製品の需要予測や在庫管理に活用されます。

季節性とトレンド

季節性とトレンドは時系列データの重要な要素です。季節性は、1年の特定の時期に観測されるパターン、例えばクリスマス前の売上増加などを指します。一方、トレンドは、より長い期間にわたるデータの上昇や下降の傾向を指します。これらは乗法モデルで表されることが多く、これはデータの季節的変動が時間とともに増減することを表します。

次のセクションでは、これらの概念を実際の例に適用し、Pythonを使ってどのようにデータを分析するかを見ていきます。私たちはstatsmodelsという強力なツールを用いて、データを詳細に分析し、有益な洞察を抽出する方法を学んでいきます。実際のグラフを用いた分析は次のステップで紹介しますので、その準備として、まずは時系列データの基本をしっかりと理解しましょう。

時系列分析を始めるにあたり、Pythonで使える強力なライブラリの一つにstatsmodelsがあります。このライブラリを使うと、統計モデルを構築し、統計テストを実行し、データを探索・分析できます。特に時系列データの分析においては、データのトレンドや季節性などを見つけ出し、未来のデータを予測するのに役立ちます。

statsmodelsのインストール

まず最初に、statsmodelsを使うためには、Python環境にインストールする必要があります。ほとんどの場合、pipコマンドで簡単にインストールできます。

pip install statsmodels

のコマンドを実行することで、statsmodelsライブラリがあなたのコンピュータにダウンロードされ、インストールされます。

成分分解の基本

時系列データを分析する際には、データをその構成要素に分解することがしばしば行われます。このプロセスを「成分分解」と呼びます。具体的には、データからトレンド（長期的な変動）、季節性（定期的な変動）、残差（その他の変動）を抽出することを指します。

Pythonで成分分解を行うには、まずサンプルデータが必要です。ここでは、単純化のために、短い期間の気温データを模擬的に生成してみましょう。

import numpy as np
import pandas as pd
from statsmodels.tsa.seasonal import seasonal_decompose
import matplotlib.pyplot as plt

# 2023年の日付範囲を生成
date_range = pd.date_range(start='2023-01-01', end='2023-12-31', freq='D')

# 正弦波を使って、夏が暑く冬が寒い気温データを模擬
# np.cosを使って1年を通じての気温変化を模擬し、中心を20度に設定
data = 20 + np.cos(np.linspace(0, 2 * np.pi, len(date_range))) * -10  # 冬が寒く、夏が暑い
data += np.random.normal(0, 3, len(date_range))  # ランダムなノイズを追加

# pandasのSeriesとして時系列データを作成
time_series = pd.Series(data, index=date_range)

# 成分分解の実行
result = seasonal_decompose(time_series, model='additive')

# 結果のプロット
result.plot()
plt.show()

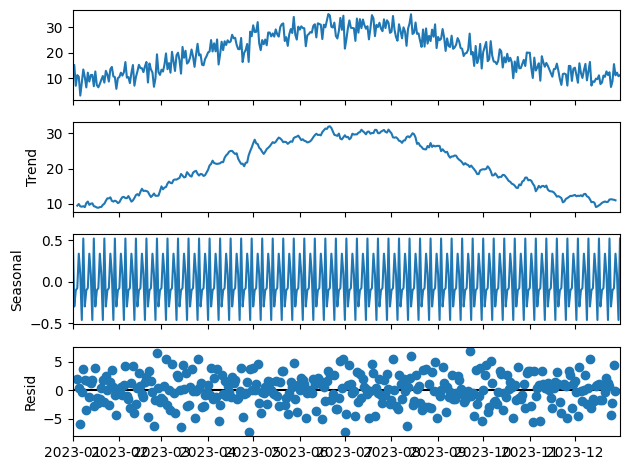
このコードは、seasonal_decompose関数を用いて時系列データを成分分解し、結果をグラフで表示します。グラフからは、データのトレンド、季節性、そして残差が視覚的に理解できます。

このプロセスを通じて、時系列データの基本的な特性を探ることができます。次のセクションでは、このデータをさらに深く分析し、どのようにして時系列データから有益な情報を引き出すかを見ていきます。

時系列データの視覚化

時系列データの分析では、データの視覚化が重要な役割を果たします。視覚化によって、データのトレンド、季節性、異常値などを直感的に理解することができます。このセクションでは、Pythonを使用して時系列データを視覚化するいくつかの方法について紹介します。

時系列グラフの基本

時系列データをプロットする基本的な方法から始めます。Pythonのmatplotlibライブラリを使用すると、データを簡単にグラフにすることができます。

import matplotlib.pyplot as plt

# フォント設定
plt.rcParams['font.family'] = 'Meiryo'  

# サンプルデータの時系列グラフをプロット
plt.figure(figsize=(10, 6))
plt.plot(time_series.index, time_series, label='気温')
plt.title('2023年の気温変動')
plt.xlabel('日付')
plt.ylabel('気温 (°C)')
plt.legend()
plt.show()

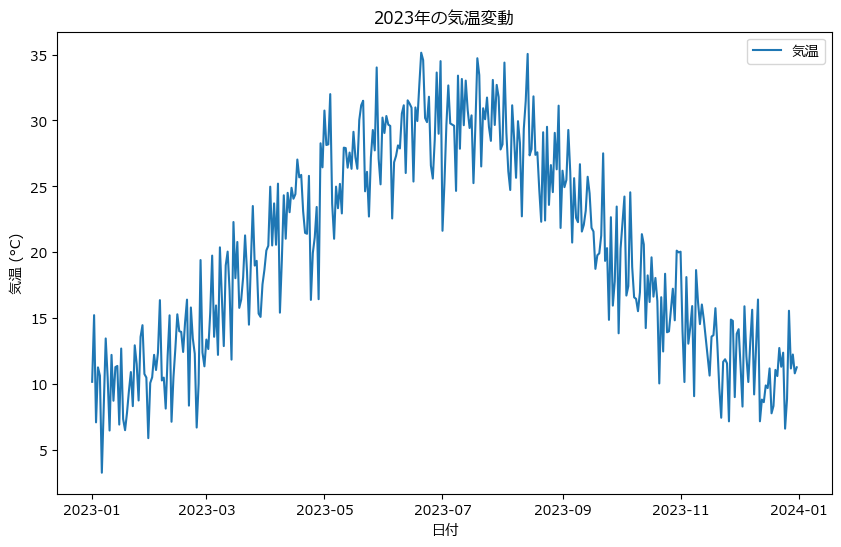
この基本的なグラフでは、年間を通じた気温の変動を視覚的に捉えることができます。特に、夏に最高気温、冬に最低気温を記録するパターンが明確に見て取れます。

コレログラムによる自己相関の分析

時系列データの特性をさらに深く理解するためには、自己相関を調べることが有効です。自己相関とは、時系列データ内の異なる時点の値がどのように関連しているかを示す指標です。statsmodelsライブラリのplot_acf関数を使用して、コレログラムを描画してみましょう。

from statsmodels.graphics.tsaplots import plot_acf

# コレログラムのプロット
plot_acf(time_series)
plt.show()

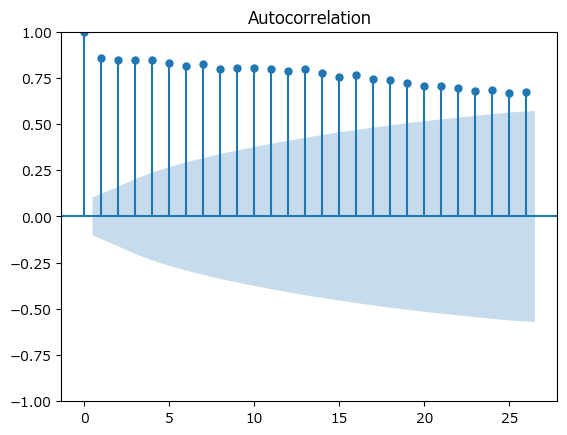
コレログラムは、時系列データの各ラグ（時間差）における自己相関を示すグラフです。自己相関とは、時系列データの異なる時点間での相関のことを指し、データポイントが時間的にどの程度関連しているかを数値化したものです。

コレログラムを見る際には以下の点に注意して解釈します：

ラグ0の自己相関：

ラグ0での自己相関は常に1です。これは、データポイントが自分自身と完全な正の相関を持つためです。

自己相関の振幅：

コレログラムの縦軸は自己相関の強さを表し、-1から1の範囲で示されます。値が1に近いほど強い正の相関、-1に近いほど強い負の相関を意味します。値が0に近い場合、相関はほとんどないと考えられます。

自己相関の減衰：

上のグラフでは、ラグが増加するにつれて自己相関の値が徐々に減少している様子が見られます。これは、時間が経過するにつれてデータポイント間の関連性が弱まっていることを示しています。

周期性の特定：

コレログラムで一定の間隔でピークが現れる場合、それはデータに周期性があることを示しています。例えば、ピークが毎12ラグごとに現れる場合、データには12単位の周期性があると解釈できます。

信頼区間：

グラフには通常、自己相関が統計的に有意であるかを示すための信頼区間（コレログラムの周りの薄い帯）が描かれています。自己相関の棒がこの帯を超えている場合、そのラグにおける自己相関は統計的に有意であり、偶然の結果ではないと考えられます。

上のコレログラムにおいて、多くのラグで自己相関が信頼区間を超えていることが確認できます。これは、時系列データが強い周期性を持っていることを示唆しています。また、自己相関が徐々に減少していることから、これらの周期的な変動は時間とともに影響が減少していく傾向にあることも読み取れます。この情報は、データに季節性や他の定期的なパターンが含まれていることを示唆しており、この分析は予測モデルを構築する際に非常に有益な情報となります。

外れ値の視覚化

時系列データにおける外れ値は、異常な気象現象や計測ミスなど、さまざまな原因で発生することがあります。外れ値を視覚化することで、これらの異常値を迅速に識別し、分析における考慮事項とすることができます。matplotlibのfill_between関数を使用して、特定の条件下でのデータポイントを強調表示する方法を紹介します。

# 外れ値を強調表示するグラフの作成
plt.figure(figsize=(10, 6))
plt.plot(time_series.index, time_series, label='気温')
plt.fill_between(time_series.index, time_series, where=(time_series < 10), color='blue', alpha=0.3, label='低温')
plt.fill_between(time_series.index, time_series, where=(time_series > 30), color='red', alpha=0.3, label='高温')
plt.title('2023年の気温変動と外れ値の視覚化')
plt.xlabel('日付')
plt.ylabel('気温 (°C)')
plt.legend()
plt.show()

この方法を用いることで、特に低温や高温といった外れ値を直感的に捉え、分析の際の重要な手がかりとすることができます。今回の例では異常値がなかったため、10℃未満、あるいは30℃超といった値を外れ値とみなしていますが、実際には気温としては不適切な値などを検知する際などに利用可能です。

時系列データの予測モデル構築

次に時系列データを予測するためのモデル構築に移りますが、まずはどのようなモデルがあるかを見てみたいと思います。

一般的な時系列モデルの概観

時系列分析にはさまざまなアプローチが存在します。ここでは、主に使用されるモデルの種類とその特徴を簡単に解説します。

移動平均モデル (MA)

移動平均モデルは、過去の予測誤差の平均を利用して未来の値を予測します。シンプルで理解しやすいモデルですが、複雑な時系列データのパターンを捉えるには限界があります。

自己回帰モデル (AR)

自己回帰モデルは、過去の値を利用して未来の値を予測します。時系列データの自己相関を基にした予測を行うため、周期性やトレンドを持つデータに適しています。

統合移動平均自己回帰モデル (ARIMA)

ARIMAモデルは、自己回帰モデルと移動平均モデルの特徴を組み合わせ、さらに非定常性を扱うことができるようにしたモデルです。トレンドや季節性を取り除いたデータの予測に有効です。

季節調整統合移動平均自己回帰モデル (SARIMA)

SARIMAモデルは、ARIMAモデルに季節成分を加えたものです。季節性を持つ時系列データの分析に特に適しており、予測精度の向上が期待できます。

ベクトル自己回帰モデル (VAR)

複数の時系列データが相互に影響し合う場合に使用されるモデルです。各時系列データを同時に分析し、予測することが可能です。

ディープラーニングモデル

LSTM（Long Short-Term Memory）などのディープラーニングモデルは、非線形な時系列データや複雑なパターンを持つデータの予測に有効です。大量のデータから学習する能力が高い反面、モデルの解釈性には課題があります。

ARIMAモデルの理解と実装

時系列データの予測には様々な手法が存在しますが、特にARIMAモデルはその精度の高さから広く利用されています。ここでは、ARIMAモデルの基本構造と、Pythonでの簡単な実装方法を見ていきましょう。

概要

ARIMA（AutoRegressive Integrated Moving Average）モデルは、時系列データの分析と予測に広く用いられる強力なモデルです。このモデルは、データの非定常性を取り除くために差分を取る「統合（I）」、過去の値に基づいて未来を予測する「自己回帰（AR）」、そして過去の予測誤差を利用する「移動平均（MA）」の3つの要素から成り立っています。

ARIMAモデルの構成要素

• **AR（自己回帰）**部分は、時系列データの過去の値が未来の値にどのように影響するかをモデル化します。パラメータpは、モデルが参照する過去の観測値の数を指します。
• **I（統合）**部分は、時系列データを差分して非定常性を取り除くプロセスを表します。パラメータdは、差分を取る回数を指します。
• **MA（移動平均）**部分は、モデルの誤差項が過去の予測誤差にどのように影響されるかをモデル化します。パラメータqは、誤差項のモデリングに使用される過去の誤差項の数を指します。

ARIMAモデルの実装例

Pythonのstatsmodelsライブラリを用いて、簡単なARIMAモデルを実装し、時系列データの予測を行う例を紹介します。まずは、適切なパラメータ（p, d, q）を選択することが重要です。

import numpy as np
import pandas as pd
from statsmodels.tsa.arima.model import ARIMA
import matplotlib.pyplot as plt

# サンプルデータの生成（ここでは簡単な時系列データを想定）
np.random.seed(42)
data = np.random.randn(100).cumsum()

# pandas Seriesに変換
time_series = pd.Series(data)

# ARIMAモデルの定義とフィット
# ここではp=2, d=1, q=2としてみます
model = ARIMA(time_series, order=(2, 1, 2))
model_fit = model.fit()

# 未来の値を予測
forecast = model_fit.forecast(steps=10)

# 元の時系列データと予測値のプロット
plt.figure(figsize=(10, 6))
plt.plot(time_series, label='Original')
plt.plot(np.arange(len(time_series), len(time_series) + 10), forecast, label='Forecast')
plt.title('Time Series Forecasting with ARIMA')
plt.xlabel('Time')
plt.ylabel('Value')
plt.legend()
plt.show()

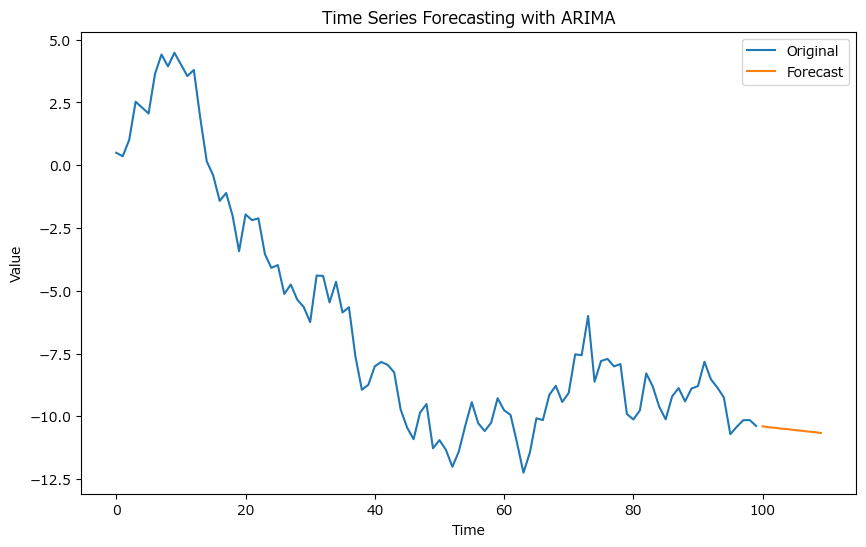
このコード例では、ARIMAモデルを定義し、フィットさせた後に未来の値を予測しています。実際のデータ分析では、まずデータの観察、次に適切なp, d, qの選択、そしてモデルの診断を行い、最適なモデルを決定するプロセスが重要になります。

モデルの選択と評価

ARIMAモデルのパフォーマンスを評価し、適切なパラメータを選択するには、AIC（赤池情報量基準）やBIC（ベイズ情報量基準）などの統計的指標を参照することが一般的です。これらの指標は、モデルの複雑さとデータへの適合度をバランス良く評価するためのものです。

季節性を考慮した時系列分析：SARIMAモデル

時系列データにおいて季節性のパターンは一般的であり、これを考慮に入れた予測モデルを構築することが、予測の精度を高める鍵になります。SARIMAモデルは、ARIMAモデルを拡張し、季節性の影響を含む時系列データの分析と予測を可能にします。

SARIMAモデルの基本構造

SARIMAモデルは、(p, d, q)×(P, D, Q, S)という形式で表され、季節性と非季節性の両方の要素をモデル化します。ここで、p, d, qは非季節的成分を示し、P, D, Qは季節的成分を示し、Sは季節の期間を表します。この複合的な構造により、SARIMAモデルはより複雑な時系列データのパターンを捉えることができます。

PythonでのSARIMAモデルの実装

statsmodelsライブラリを使用することで、Pythonで簡単にSARIMAモデルを実装し、時系列データの予測を行うことができます。以下は、SARIMAモデルの基本的な実装例です。

import numpy as np
import pandas as pd
from statsmodels.tsa.statespace.sarimax import SARIMAX
import matplotlib.pyplot as plt

# サンプル時系列データの生成
np.random.seed(42)
data = np.sin(np.linspace(0, 2 * np.pi, 24)) + np.random.normal(0, 0.1, 24)
time_series = pd.Series(data, index=pd.date_range(start="2023-01-01", periods=24, freq="M"))

# SARIMAモデルの定義とフィット
# ここでは、非季節性成分としてp=1, d=1, q=1、季節性成分としてP=1, D=1, Q=1, S=12を使用
model = SARIMAX(time_series, order=(1, 1, 1), seasonal_order=(1, 1, 1, 12))
model_fit = model.fit()

# 未来の値を予測
forecast = model_fit.forecast(steps=12)

# 元の時系列データと予測値のプロット
plt.figure(figsize=(10, 6))
plt.plot(time_series, label='Original')
plt.plot(forecast, label='Forecast', linestyle='--')
plt.title('Time Series Forecasting with SARIMA')
plt.legend()
plt.show()

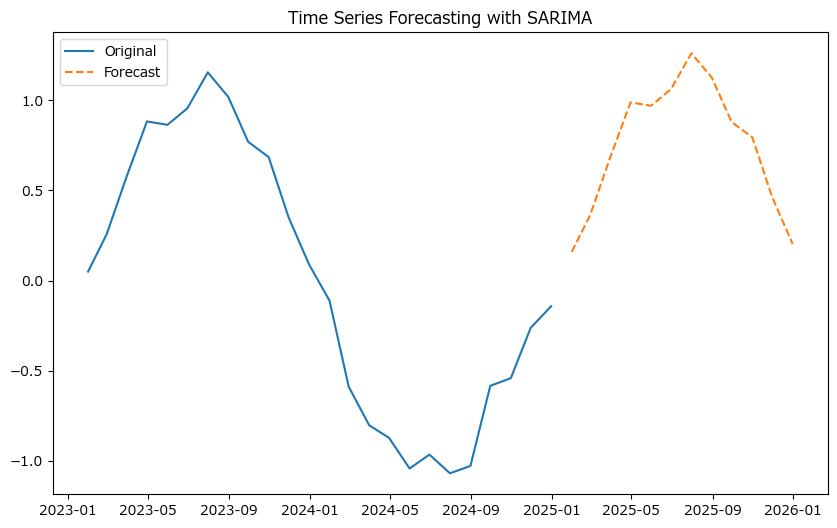
この例では、24ヶ月のデータに基づいて次の12ヶ月の予測を行っています。SARIMAモデルの季節的オーダーは、データに見られる季節性のパターンに基づいて選択されます。

SARIMAモデルの応用

SARIMAモデルは、季節性の影響が顕著な時系列データ、例えば小売業の月間売上や気象データの分析に特に有効です。適切なパラメータを選択することで、データの季節性パターンを正確にモデル化し、将来の時点での値を予測することができます。

ディープラーニングによる時系列予測

近年、ディープラーニングは多くの領域で注目されており、時系列データの予測においても例外ではありません。ディープラーニングモデル、特にLSTMは、その長期依存性を捉える能力により、時系列予測の分野で非常に効果的です。このセクションでは、LSTMモデルの基本的な概念と、Pythonを使った実装例を紹介します。

LSTMモデルの概念

LSTM（Long Short-Term Memory）は、従来のリカレントニューラルネットワーク（RNN）の問題である「長期依存性の問題」を解決するために開発されました。LSTMは特殊な種類のRNNであり、長期的な依存関係を学習する能力があります。これは、時系列データのように時間的に連続するデータを扱う際に特に有効です。

PythonによるLSTMモデルの実装

PythonのKerasライブラリを使用して、LSTMモデルを簡単に実装することができます。ここでは、簡単な時系列データに対するLSTMモデルの構築と学習のプロセスを示します。

from keras.models import Sequential
from keras.layers import LSTM, Dense
import numpy as np

# サンプルデータの生成（例として正弦波を使用）
timesteps = 100
data = np.sin(np.linspace(0, 2 * np.pi, timesteps))

# データの前処理
# LSTMに入力するためのデータ形状に変換する必要があります
X = data[:-1].reshape(1, timesteps - 1, 1)
y = data[1:].reshape(1, timesteps - 1, 1)

# モデルの定義
model = Sequential()
model.add(LSTM(50, activation='relu', input_shape=(timesteps - 1, 1)))
model.add(Dense(1))
model.compile(optimizer='adam', loss='mse')

# モデルの学習
model.fit(X, y, epochs=200, verbose=0)

# 予測値の生成
predicted = model.predict(X)

# 実データと予測データのプロット
import matplotlib.pyplot as plt

plt.plot(data[1:], label='Actual')
plt.plot(predicted.flatten(), label='Predicted')
plt.title('LSTM Time Series Prediction')
plt.legend()
plt.show()

このコード例では、LSTMモデルを使用して単純な時系列データの次のステップを予測しています。実際の応用では、より複雑なデータセットや、複数の特徴を持つ時系列データに対してもこのアプローチを適用することが可能です。

LSTMモデルの応用

LSTMモデルは、金融市場の予測、気象予報、言語モデリングなど、様々な分野で応用されています。その強力な時系列データの学習能力により、複雑な時系列パターンを予測する際に有効なツールとなります。

この記事を通じて、時系列データ分析の基礎からディープラーニングによる予測までを見てきました。今回は入門の内容でしたが、これをきっかけに実践を積んで精度の高いモデルを構築してもらえたら嬉しいです。