Pythonを使用して経度・緯度のデータを効果的に活用する方法は、データ分析やアプリケーション開発で役立ちます。今回の記事では、Pythonを使用して経度・緯度からの距離計算や地図上のプロット方法について解説します。
Pythonを使った経度・緯度からの距離計算
基本的な距離計算の原理
地球はほぼ球形であるため、2点間の距離を計算する際には平面的な計算ではなく、球面上の距離を考慮する必要があります。このとき使用されるのが「ハヴァサイン公式」というものです。
ハヴァサイン公式とは
ハヴァサイン公式は、球面上の2点間の最短距離を計算するための公式です。数式で表すと以下のようになりますがここでは詳細は省きます。
$$a = \sin^2\left(\frac{\Delta \text{lat}}{2}\right) + \cos(\text{lat}_1) \cdot \cos(\text{lat}_2) \cdot \sin^2\left(\frac{\Delta \text{lon}}{2}\right)$$
$$c = 2 \cdot \text{atan2}\left(\sqrt{a}, \sqrt{1-a}\right)$$
$$d = R \cdot c$$
- Δlatは2点間の緯度の差
- Δlonは2点間の経度の差
- R は地球の半径 (約6371km)
コード例
上記式より、2点の経度・緯度から距離を計算する関数は以下のように定義できます。
import math
def calc_distance(lat1, lon1, lat2, lon2):
R = 6371.0 # 地球の半径 (km)
dlat = math.radians(lat2 - lat1) # 緯度の差をラジアンに変換
dlon = math.radians(lon2 - lon1) # 経度の差をラジアンに変換
# ハヴァサイン公式の計算
a = math.sin(dlat / 2)**2 + math.cos(math.radians(lat1)) * math.cos(math.radians(lat2)) * math.sin(dlon / 2)**2
c = 2 * math.atan2(math.sqrt(a), math.sqrt(1 - a))
return R * c # 距離を返す
この関数を用いて、例として東京と大阪の間の距離を計算してみましょう。
# 東京の緯度・経度
lat1, lon1 = 35.6895, 139.6917
# 大阪の緯度・経度
lat2, lon2 = 34.6937, 135.5023
# 距離の計算
distance = calc_distance(lat1, lon1, lat2, lon2)
print(f"東京と大阪の間の距離は約{distance:.2f}kmです。")
東京と大阪の間の距離は約396.44kmです。経度・緯度を地図上にプロットする方法
Pythonでは経度と緯度の情報を地図上にプロットすることで、データの位置的な関係を視覚的に理解することができます。foliumというライブラリを使用すると、簡単に地図上にデータをプロットすることができます。
import folium
# 地図の中心となる経度・緯度を指定して、地図を作成
m = folium.Map(location=[35.6895, 139.6917], zoom_start=7)
# マーカーを追加
folium.Marker([35.6895, 139.6917], tooltip='東京').add_to(m)
folium.Marker([34.6937, 135.5023], tooltip='大阪').add_to(m)
# 地図を表示
m
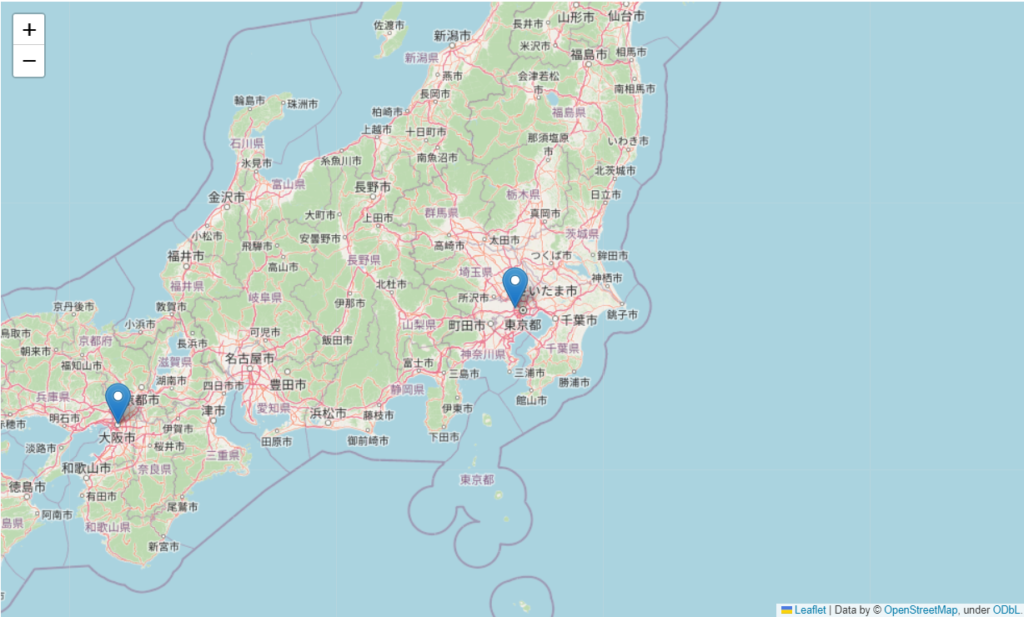
位置情報は今後も多くのアプリケーションやサービスで重要な役割を果たすでしょう。Pythonを使って簡単に経度・緯度のデータを活用する方法を学ぶことで、より高度なデータ分析やアプリケーション開発が可能になります。今回の記事が、Pythonを使用した位置情報の活用に関する入門として役立てば幸いです。



