機械学習モデルの評価は、モデルの性能を理解し改善するために不可欠なプロセスです。Pythonの機械学習ライブラリであるscikit-learnは、モデルの評価を行うための便利な関数を提供しています。この記事では、scikit-learnを使用して機械学習モデルの評価を行う方法について解説します。
AccuracyScoreの使用方法
scikit-learnのaccuracy_score関数を使用して、分類モデルの精度を計算することができます。この関数は、予測ラベルと正解ラベルの一致率を計算し、その値を返します。
以下に、シンプルなデータを用いた使用例を示します。
from sklearn.metrics import accuracy_score
# 予測ラベル
y_pred = [0, 2, 1, 3]
# 正解ラベル
y_true = [0, 1, 2, 3]
# accuracyの算出
print(accuracy_score(y_true, y_pred)) # 出力:0.5
この例では、予測と正解ラベルのうち一致しているものが4分の2となっているため、0.5と算出されます。accuracy_score関数の引数は、正解ラベルと予測ラベルの順番になっていることに注意してください。
また、normalize引数をFalseに設定すると、正しく分類されたサンプル数を返します。デフォルトはTrueで、正しく分類されたサンプルの割合(精度)を返します。
print(accuracy_score(y_true, y_pred, normalize=False)) # 出力:2
このように、accuracy_score関数はモデルの性能を評価する際に非常に便利なツールです。
ConfusionMatrix【混合行列】の理解と作成
混合行列(Confusion Matrix)は、分類問題の結果を「実際のクラス」と「予測したクラス」を軸にしてまとめたものです。2値分類においては、以下の4種類に結果を分けることができます。
- 真陽性(TP: True Positive): 実際のクラスが陽性で予測も陽性(正解)
- 真陰性(TN: True Negative): 実際のクラスが陰性で予測も陰性(正解)
- 偽陽性(FP: False Positive): 実際のクラスは陰性で予測が陽性(不正解)
- 偽陰性(FN: False Negative): 実際のクラスは陽性で予測が陰性(不正解)
これらを行列形式で表したものが混合行列です。以下にその例を示します。
| 予測/実際 | Negative | Positive |
|---|---|---|
| Negative | TN | FN |
| Positive | FP | TP |
混合行列は、scikit-learnのconfusion_matrix関数を用いて作成します。以下にその例を示します。
from sklearn.metrics import confusion_matrix
# 正解ラベル
y_true = [0, 0, 0, 0, 0, 1, 1, 1, 1, 1]
# 推定ラベル
y_pred = [0, 1, 1, 1, 1, 0, 0, 0, 1, 1]
# 混合行列の作成
cm = confusion_matrix(y_true, y_pred)
print(cm)
# 出力:
# [[1 4]
# [3 2]]
このままでは見にくいので、混合行列を可視化します。可視化には、seabornライブラリのheatmap関数を用います。
import seaborn as sns
import matplotlib.pyplot as plt
# ヒートマップの作成
sns.heatmap(cm, annot=True,cmap='Blues')
plt.show()
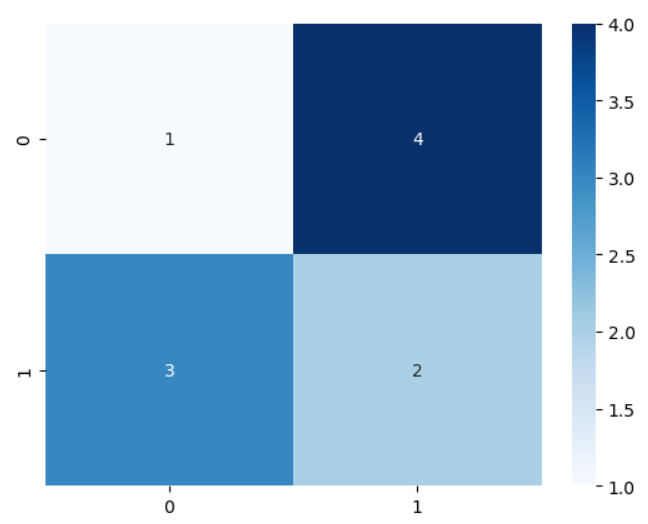
これにより、混合行列の各要素の値を色の濃淡で視覚的に理解することができます。
分類問題の評価指標:ClassificationReport
ClassificationReportは、分類問題の結果を様々な指標に基づいて集計したテキストレポートです。scikit-learnのclassification_report関数を用いて作成します。この関数は第1引数に正解ラベル、第2引数に予測ラベル、第3引数に目的変数の各クラスの名前を指定します。
以下に、シンプルなデータに対するClassificationReportの作成例を示します。
from sklearn.metrics import classification_report
# 正解ラベル
y_true = [0, 1, 2, 2, 2]
# 推定ラベル
y_pred = [0, 0, 2, 2, 1]
# 目的変数の各クラス名
target_names = ['class 0', 'class 1', 'class 2']
print(classification_report(y_true, y_pred, target_names=target_names))
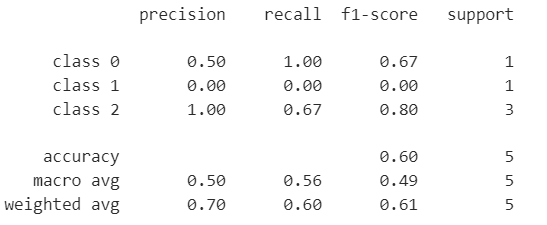
ここでprecisionは適合率(モデルが正と予測したもののうち、実際に正であったものの割合)、recallは再現率(実際に正であるもののうち、モデルが正と予測したものの割合)を示します。これら2つの指標はトレードオフの関係にあります。またf1-scoreは適合率と再現率の調和平均で、両方の指標をバランス良く評価したい場合に用いられます。
さらにmicro avg(マイクロ平均)、macro avg(マクロ平均)、weighted avg(加重平均)は、それぞれレコードとクラスのペアごとの平均、各クラスごとの平均、各クラスごとの加重平均を示します。これらは比較的使用頻度が少ない評価指標です。
ClassificationReportは、モデルの性能を多角的に評価するのに役立ちます。Precision、Recall、F1-scoreはそれぞれ異なる観点からモデルの性能を評価します。Precisionは偽陽性の数を最小限に抑えることが重要な場合(例えば、スパムメールのフィルタリング)、Recallは偽陰性の数を最小限に抑えることが重要な場合(例えば、病気の早期発見)、F1-scoreはPrecisionとRecallのバランスを取ることが重要な場合に特に有用です。
以上がClassificationReportの基本的な説明と使用方法です。これらの指標を理解し、適切に活用することで、分類モデルの性能をより深く理解することができます。
回帰問題の評価指標:MeanAbsoluteError(平均絶対誤差)
MeanAbsoluteError(MAE)は回帰問題の評価指標の一つで、予測値と実際の値との誤差の絶対値の平均を示します。scikit-learnのmean_absolute_error関数を用いて計算します。この関数は、第1引数に正解ラベル、第2引数に予測ラベルを指定します。
以下に、シンプルなデータに対するMAEの計算例を示します。
from sklearn.metrics import mean_absolute_error
# 正解値
y_true = [3, -0.5, 2, 7]
# 予測値
y_pred = [2.5, 0.0, 2, 8]
# MAEの算出
print(mean_absolute_error(y_true, y_pred))
出力結果は0.5となります。これは予測値と実際の値との誤差の絶対値の平均が0.5であることを示しています。
また実際のデータセットを用いてモデルを作成し、そのモデルのMAEを計算することで、モデルの性能を評価することができます。例えば糖尿病の診断データセットを使用してK近傍法によるモデルを作成し、そのモデルのMAEを計算することができます。
以上がMeanAbsoluteErrorの基本的な説明と使用方法です。この指標を理解し適切に活用することで、回帰モデルの性能をより深く理解することができます。
回帰問題の評価指標:MeanSquaredError(平均二乗誤差)
MeanSquaredError(MSE)は、回帰問題の評価指標の一つで、予測値と実際の値との誤差の二乗の平均を示します。大きな誤差が存在する場合、MSEはその誤差をより強調します。つまり、MSEの値が大きいほど、モデルの誤差が大きいことを示します。
scikit-learnのmean_squared_error関数を用いてMSEを計算します。この関数は、第1引数に正解ラベル、第2引数に予測ラベルを指定します。
以下に、シンプルなデータに対するMSEの計算例を示します。
from sklearn.metrics import mean_squared_error
# 正解値
y_true = [3, -0.5, 2, 7]
# 予測値
y_pred = [2.5, 0.0, 2, 8]
# MSEの算出
print(mean_squared_error(y_true, y_pred))
出力結果は0.375となります。これは、予測値と実際の値との誤差の二乗の平均が0.375であることを示しています。
また、MSEの平方根を取ったものをRoot Mean Squared Error(RMSE)と呼びます。RMSEはMSEが二乗により誤差を過大評価する傾向を補正した評価指標となります。scikit-learnにはRMSEの計算関数は用意されていませんが、numpyのnp.sqrt()関数を用いて簡単に計算することができます。
import numpy as np
from sklearn.metrics import mean_squared_error
# 正解値
y_true = [3, -0.5, 2, 7]
# 予測値
y_pred = [2.5, 0.0, 2, 8]
# RMSEの算出
print(np.sqrt(mean_squared_error(y_true, y_pred)))
出力結果は約0.612となります。これは、予測値と実際の値との誤差の二乗の平均の平方根(つまり、RMSE)が約0.612であることを示しています。
以上が、MeanSquaredErrorとRoot Mean Squared Errorの基本的な説明と使用方法です。これらの指標を理解し、適切に活用することで、回帰モデルの性能をより深く理解することができます。
回帰問題の評価指標:R²Score(決定係数)
R²Score(決定係数)は、独立変数(説明変数)が従属変数(目的変数)をどれだけ説明できるかを示す指標で、統計学においてよく用いられます。最も予測が正確な場合、R²Scoreは1.0となります。つまり、R²Scoreが大きいほど、モデルの予測精度が高いと言えます。
scikit-learnのr2_score関数を用いてR²Scoreを計算します。この関数は、第1引数に正解ラベル、第2引数に予測ラベルを指定します。
以下に、シンプルなデータに対するR²Scoreの計算例を示します。
from sklearn.metrics import r2_score
# 正解値
y_true = [3, -0.5, 2, 7]
# 予測値
y_pred = [2.5, 0.0, 2, 8]
# R²Scoreの算出
print(r2_score(y_true, y_pred))
出力結果は約0.9486となります。これは、予測値が実際の値を約94.86%説明できていることを示しています。
以上が、R²Score(決定係数)の基本的な説明と使用方法です。この指標を理解し、適切に活用することで、回帰モデルの性能をより深く理解することができます。
回帰問題の評価指標としては、上に見たようにMAE、MSE、RMSE、R²などがあります。MAEは予測誤差の絶対値の平均で、大きな誤差と小さな誤差を同等に扱います。一方、MSEとRMSEは大きな誤差を重視します。これらの指標は、大きな誤差を特に避けたい場合に有用です。このうちRMSEは誤差のスケールを元の目的変数のスケールに戻すため、結果の解釈が容易になるという利点があります。これらの指標を適切に選択し、使用することで、モデルの性能をより正確に評価することができます。
今回学んだ知識を活用して、実際にscikit-learnに実装されているデータセットや、SIGNATEの練習問題、Tier限定コンペなどでモデリングを行ってみることをお勧めします。
【SIGNATE練習問題】 https://signate.jp/competitions/practice
以上、scikit-learnを使用した機械学習モデルの評価についての解説でした。これらの評価指標を理解し、適切に活用することで、モデルの性能をより深く理解し、より良いモデルを作成することができます。



