SIGNATE 【練習問題】Jリーグの観客動員数予測　への挑戦

SIGNATEの学習コースQuest「スポーツのチケット価格の最適化」の総仕上げとして、コンペの練習問題「Jリーグの観客動員数予測」に取り組みました。

回帰モデルの作成手順をまとめたこちらの記事に沿って作業を進めましたので、適宜ご参照ください。

関連記事

機械学習入門：回帰モデルの作成から評価まで

[mathjax] この記事では、機械学習の回帰モデル作成の基本的な流れを解説します。対象データの理解から始め、特徴量の選択、モデルの作成と学習、そしてモデルの評価まで、一連のステップを具体的なコード例とともに説明します。この記事に[…]

コンペの概要

このコンペティションの目的は、Jリーグ公式戦2014年シーズン後半戦の全試合の観客動員数を予測するモデルを作成することです。モデルの作成には2012年から2014年シーズン前半までのデータを使用します。J1かJ2か、平日か休日か、あるいはクラブチームの人気などに左右されることが想定されますが、それらのデータを用いて観客動員数を予測することになります。

入力データ

以下の内容のデータが与えられます。詳細は公式HPをご参照ください。

学習用：2012～2014年シーズン前半戦（～7月31日）のJリーグ（J1、J2）の各試合の観客動員数、チーム名、開催スタジアム、天候、出場メンバー、試合結果等の情報。
評価用：2014年シーズン後半戦（8月2日～11月23日）のJリーグ（J1、J2）の試合の情報。

データの読み込みと結合

以下、このコンペに際して私が行った処理について順に記載していきます。

データの読み込み

まずはinputデータがたくさんあるので一通り読み込んでデータフレームに格納します。

import pandas as pd

train_df = pd.read_csv('train.csv')
train_add_df = pd.read_csv('train_add.csv')
test_df = pd.read_csv('test.csv')
condition_df = pd.read_csv('condition.csv')
condition_add_df = pd.read_csv('condition_add.csv')
add_2014_df = pd.read_csv('2014_add.csv')
stadium_df = pd.read_csv('stadium.csv')

データの概要把握

各データの先頭5行を表示し、どのようなデータかをざっと確認しておきます。

train_df.head()

train_add_df.head()

test_df.head()

condition_df.head()

condition_add_df.head()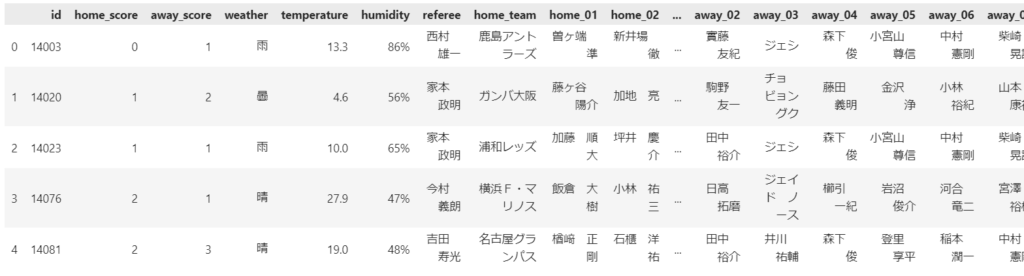

add_2014_df.head()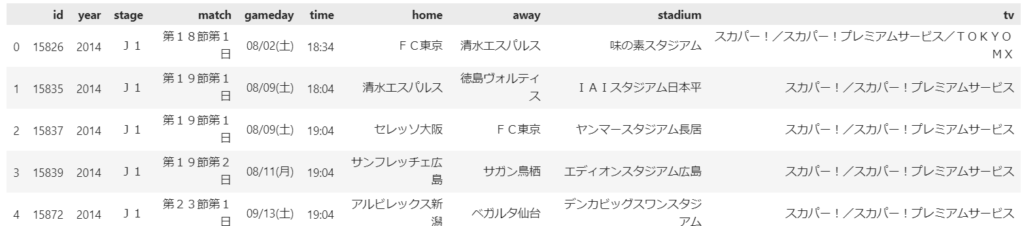

stadium_df.head()

次に各データの行列サイズを確認します。

print(train_df.shape)
print(train_add_df.shape)
print(test_df.shape)
print(condition_df.shape)
print(condition_add_df.shape)
print(add_2014_df.shape)
print(stadium_df.shape)

訓練データとテストデータ(提出データ)を合わせて2300件程度のデータ数ですね。

次に主要データの型を確認しておきます。

print(train_df.info())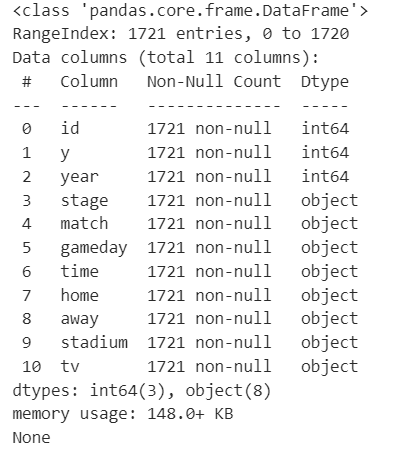

print(condition_df.info())

print(stadium_df.info())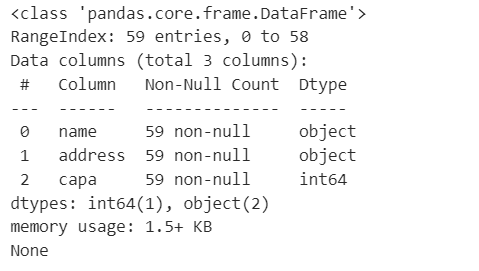

全体的にobject型が多いので後に何かしらの対応が必要になるだろうことを念頭に置いておきます。

データの結合

次にデータの結合をしていきます。まずは縦の結合から。

train_addやtrain_addについては「一部上記trainデータに抜けがありましたので、追加致します」とデータ説明があったので、縦につぎ足します。

train_df = pd.concat([train_df, train_add_df])
condition_df = pd.concat([condition_df, condition_add_df])

print(train_df.shape)
print(condition_df.shape)

次にcondition_dfは試合の詳細データということで、train_dfやtest_dfと共通のidを持っているようです。そこでこれらの2つのデータフレームはidで結合してしまいます。

train_df = pd.merge(train_df, condition_df, on='id', how='inner')
test_df = pd.merge(test_df, condition_df, on='id', how='inner')

print(train_df.shape)
print(test_df.shape)

trainデータとtestデータの数を減らすことなく結合できました。

次にstadium_dfですがこちらは各スタジアムのキャパ数が載っているので使えそうです。idはないですが、スタジアム名称でtrainやtestと結合できそうなのでしてみます。

train_df = pd.merge(train_df, stadium_df, left_on='stadium', right_on='name', how='left') 
test_df = pd.merge(test_df, stadium_df, left_on='stadium', right_on='name', how='left') 

print(train_df.shape)
print(test_df.shape)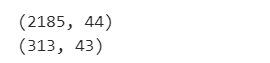

行数がそのままでカラム数が増えているので、結合に成功したことがわかります。

残るはadd_2014_dfのみなのですが、説明を読んでも回の評価対象外の期間のデータようなので、利用目的がよくわからないため、いったん使わないでおきます。

不要カラムの削除

参考記事の手順に従い、明らかに不要なカラムの削除となりますが、とりあえず上の結合の際にstadiumとnameが重複してデータフレームに残っているのでnameカラムを削除します。

train_df = train_df.drop(columns=['name'])
test_df = test_df.drop(columns=['name'])

print(train_df.columns)

以降は最初からデータ作成しなくて済むよう、いったんcsvとして保存しておきます。

train_df.to_csv("train_df.csv", index=None)
test_df.to_csv("test_df.csv", index=None)

特徴量の理解とデータ前処理

特徴量の分割とデータ変換

まず、年月曜日が１つのカラムに入っている日付データを処理しやすいようにカラムを分けます。

# 'gameday'カラムから月を抽出し、整数型に変換して新たなカラム'month'を作成
train_df['month'] = train_df['gameday'].apply(lambda x: int(x[:2]))

# 'gameday'カラムから日を抽出し、整数型に変換して新たなカラム'day'を作成
train_df['day'] = train_df['gameday'].apply(lambda x: int(x[3:5]))

# 'gameday'カラムから曜日を抽出して新たなカラム'week'を作成
train_df['week'] = train_df['gameday'].apply(lambda x: x[6:7])

# 同様に、テストデータに対しても'month', 'day', 'week'カラムを作成
test_df['month'] = test_df['gameday'].apply(lambda x: int(x[:2]))
test_df['day'] = test_df['gameday'].apply(lambda x: int(x[3:5]))
test_df['week'] = test_df['gameday'].apply(lambda x: x[6:7])

また節のカラムも「第〇節第△日」という形式のため、このままでは機械学習では扱いにくいです。そこで今回は節を取り出します。

# 'match'カラムから節数を抽出し、整数型に変換して新たなカラム'match_num'を作成します。
# これは、試合がシーズンの何節目に行われたかを表します。
train_df['match_num'] = train_df['match'].apply(lambda x: int(x[x.find("第")+1: x.find("節")]))

# テストデータに対しても同様の処理を行います。
test_df['match_num'] = test_df['match'].apply(lambda x: int(x[x.find("第")+1: x.find("節")]))

上記で作り直した元の特徴量は不要なので削除します。

train_df = train_df.drop(columns=['gameday','match'])
test_df = test_df.drop(columns=['gameday','match'])

データ形式の修正

湿度(humidity)には文字列としての%が入っていてこのままだと分析でうまく使えないので、%を除去します。

# 'humidity'カラムの値からパーセント記号を取り除き、整数に変換した後、0.01を掛けて実数に変換
train_df['humidity'] = train_df['humidity'].apply(lambda x: float(int(x[:-1])*0.01))
test_df['humidity'] = test_df['humidity'].apply(lambda x: float(int(x[:-1])*0.01))

欠損値の確認と処理

続いてデータ内に欠損値があるかどうかの確認です。

print(train_df.isnull().sum())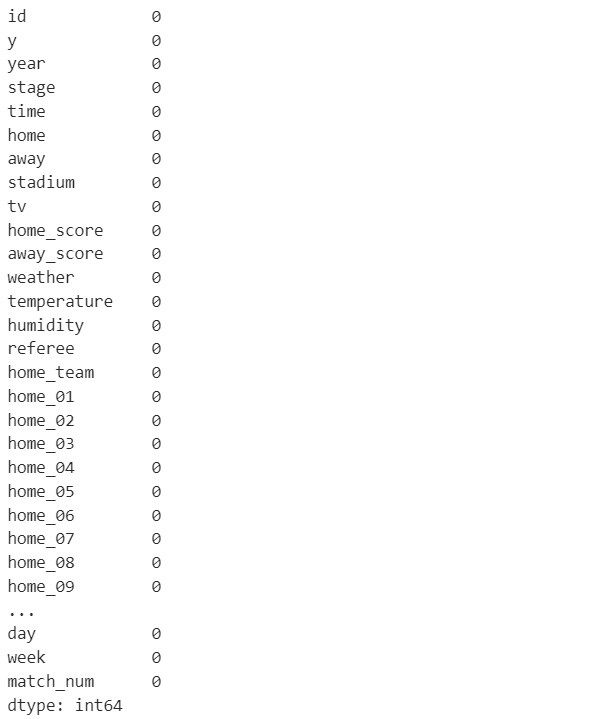

欠損値はありませんでしたので今回は欠損値処理は不要です。

説明変数の内容の確認と表記揺れの調整

次に、データの中身を確認していくとチーム名に重複があることがわかります。

train_df['home'].unique()

ザスパ草津は過去にザスパクサツ群馬へと改名していますので、これは実質同一チームです。

文字列の置換によってチーム名を統一します。

train_df = train_df.replace('ザスパ草津','ザスパクサツ群馬')
test_df = test_df.replace('ザスパ草津','ザスパクサツ群馬')

基本統計量の把握

基本統計量の確認とその解釈

全体的な統計量を見てみます。

train_df.describe()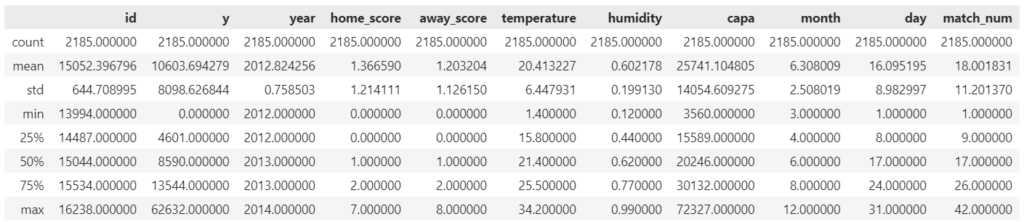

私は平均値と中央値(50%)が大きく異なるところに注目することが多いですが、その観点ではyやcapaは平均値の方がやや高く一部の大きいデータが平均を引き上げていることが推察されます。ついでにyのminが0というのも気になりますね。

外れ値の削除とその方法

さて、yが0ということは無観客ということになりますが、Jリーグではこのような無観客試合がよくあるのか、まずはy=0のデータがどれくらいあるか調べてみます。

print((train_df['y'] == 0).sum())

結果は1試合のみでした。なので外れ値として除外した方が良さそうです。

train_df = train_df[train_df['y'] > 0]

これでyが0のデータは除外されました。

データの可視化方法：ヒストグラム

表だと分布の様子がわかりにくいのでヒストグラムにしてみます。

train_df['y'].plot.hist()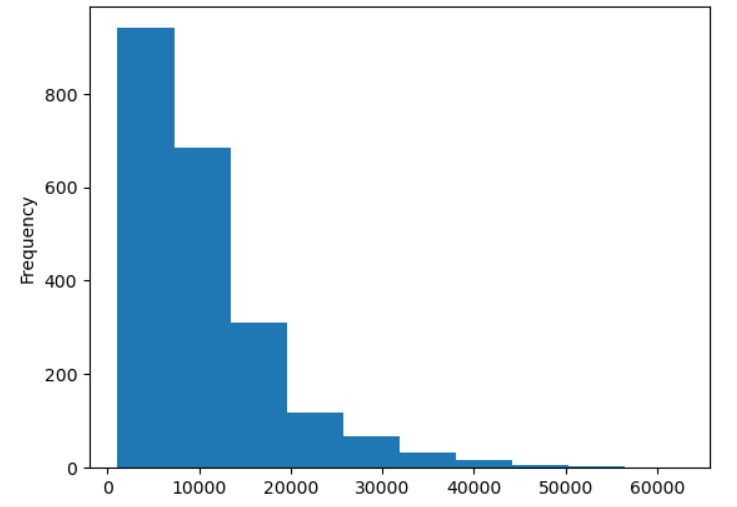

表では中央値よりも平均値の方が高かったことから一部の数値が高いデータが平均を引き上げていると考えていましたが、こうしてグラフにしてみると左側の数が低い方にデータがかなり寄っていることが一目でわかって便利ですね。

ここまできれいに左に寄っていると対数を取って正規化しておいた方が良さそうな気がするので、そうしておきます。

# log1p(numpyの関数)を適用、対数をとる
train_df["y"] = np.log1p(train_df["y"])

train_df['y'].plot.hist() #再度ヒストグラムを作成

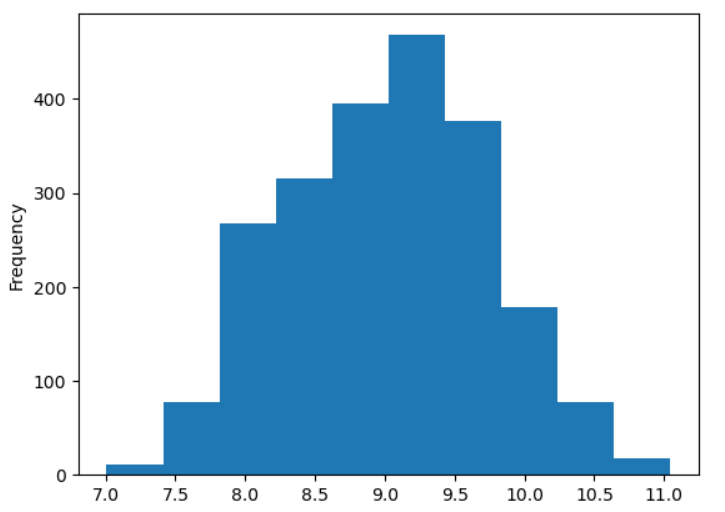
きれいに中央寄りのグラフになりましたね。

あとは同様に平均値と中央値に差があったcapaについても分布を可視化してみます。

train_df['capa'].plot.hist()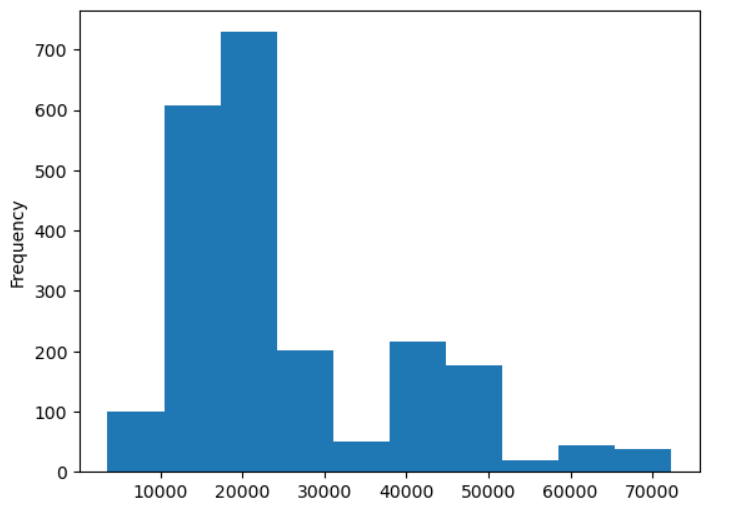

こちらはyよりはいびつな分布をしていますが、やはり低位に寄っているので正規化を施してみます。併せてtestデータも正規化しておきます。

# log1p(numpyの関数)を適用、対数をとる
train_df["capa"] = np.log1p(train_df["capa"])
test_df["capa"] = np.log1p(test_df["capa"])

train_df['capa'].plot.hist()
test_df['capa'].plot.hist()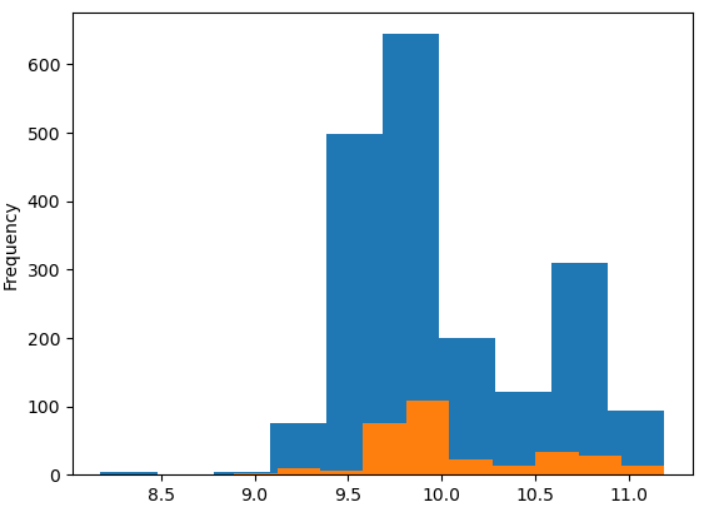

中央に寄りましたね。yと同じスケールにしておいた方が良さそうですし、このまま使ってみます。

質的データの分析：頻度値の算出と棒グラフ

質的データの方も気になったカラムの頻度はいくつか載せておきます。

train_df['year'].value_counts()

当たり前ですが、2014年の途中までが学習データの期間なので2014年が少なくなっています。ただそれ以前にテストデータに2013年以前はないのでこの特徴量は使用できませんね。

train_df['stage'].value_counts()

Ｊ１よりもＪ２の方がデータ数が多いということは頭に入れておいた方が良さそうです。

train_df['weather'].value_counts()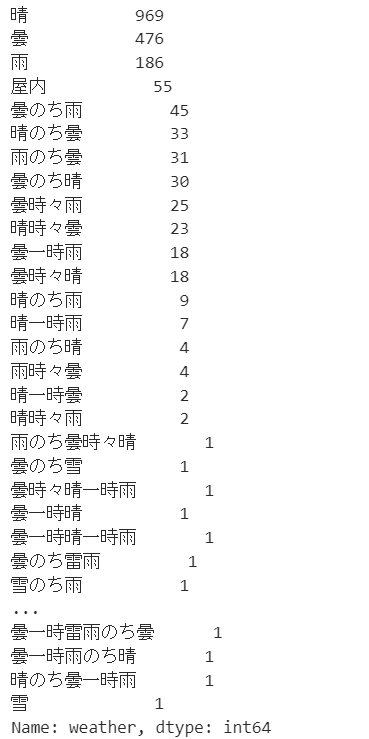

天気は細かいものまで含めると多様なデータが存在しますね。

もう少しわかりやすくするために可視化してみます。

# 日本語対応
plt.rcParams['font.family'] = 'MS Gothic'

# 頻度値を算出
counts = train_df['weather'].value_counts()

# 棒グラフの可視化
counts.plot.bar()

# 可視化結果を表示する為に必要な関数
plt.show()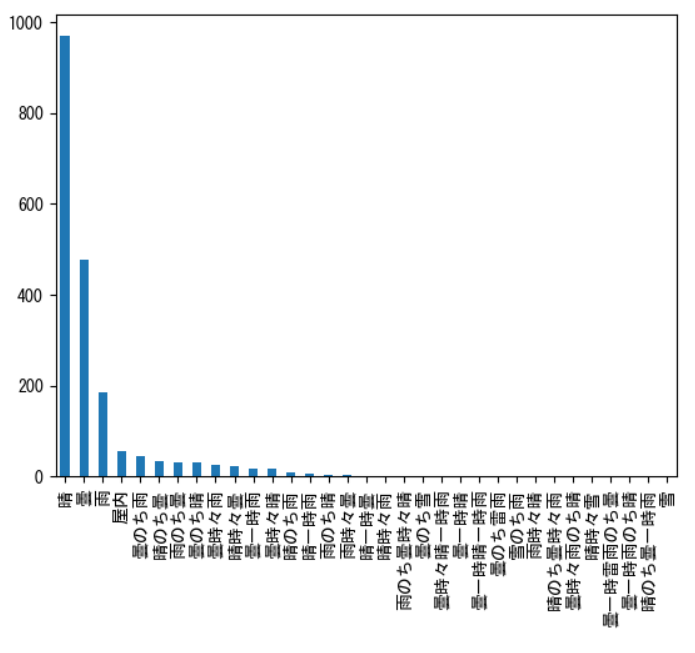

最初の数個以外は無視できるくらい小さい頻度だということがわかります。なので後半部分はまとめてしまうような処理ができそうですね。

train_df['tv'].value_counts()

テレビ放送については放送局がスラッシュで区切られている特殊な形となっており、特徴量として使用するには加工が必要だろうことが伺えます。

相関係数の確認

次に特徴量とyの関係を見ていきます。まずは量的データについて相関を確認します。

print(train_df.corr())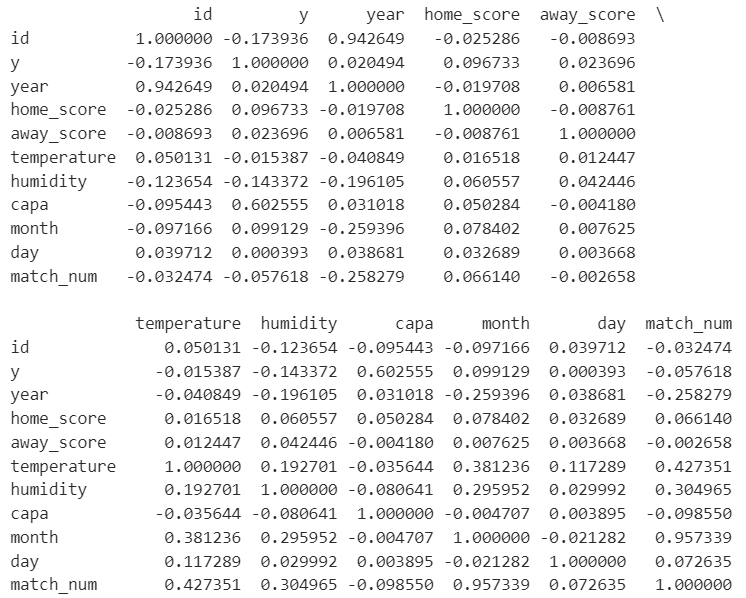

y列を見ると数値的にはcapaとの相関が高いのが目に付きます。が、わかりにくいのでヒートマップを作成してみます。

corr = train_df.corr()
plt.figure(figsize=(10, 8))  # ヒートマップのサイズを指定
sns.heatmap(corr, annot=True, cmap='coolwarm')  # ヒートマップを描画
plt.show()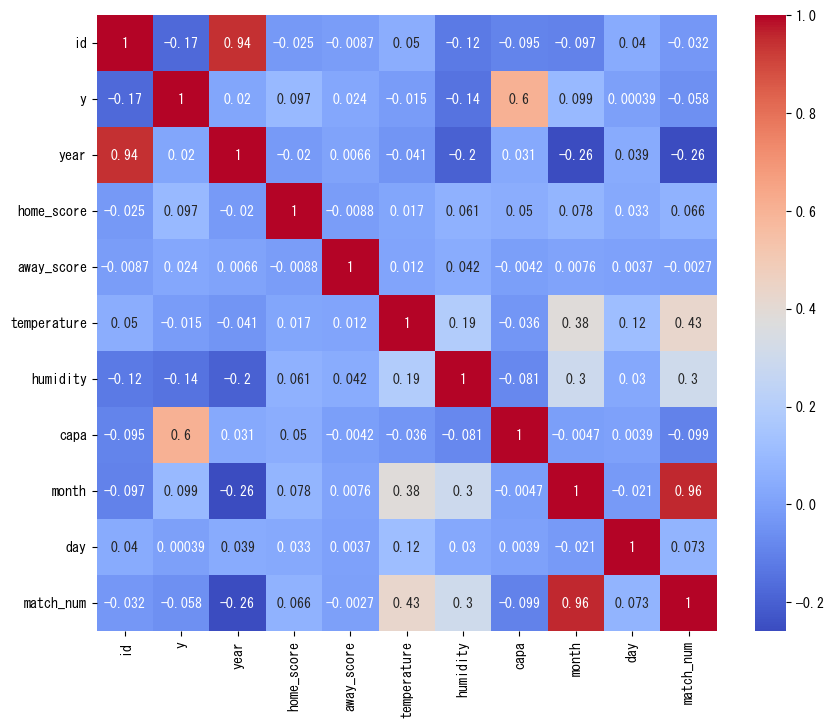

数値が高い部分を見ると、対角線は自分自身なので当たり前、month(月)とmatch_num(節)は相関があるのは納得、idは時系列だと思われるのでyearと相関があるのは当然、temperatureとmonthやmatch_numの相関も必然です。

それらを除くとcapaとyの相関の高さは際立ちますね。

次にyに関係ありそうな質的データを箱ひげ図で確認してみます。

sns.boxplot(data=train_df, x='week', y='y')
plt.show()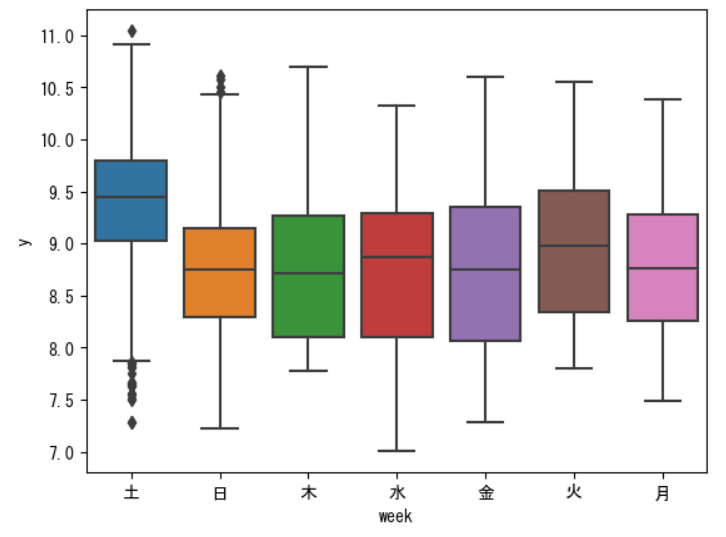

土曜日の観客数が多いのはしっくりきます。

sns.boxplot(data=train_df, x='stage', y='y')
plt.show()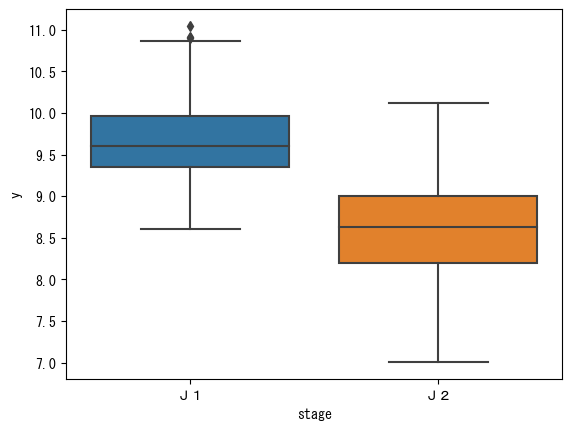

Ｊ１の方がＪ２よりも観客数が多いというのも自然な感じですよね。

sns.boxplot(data=train_df, x='month', y='y')
plt.show()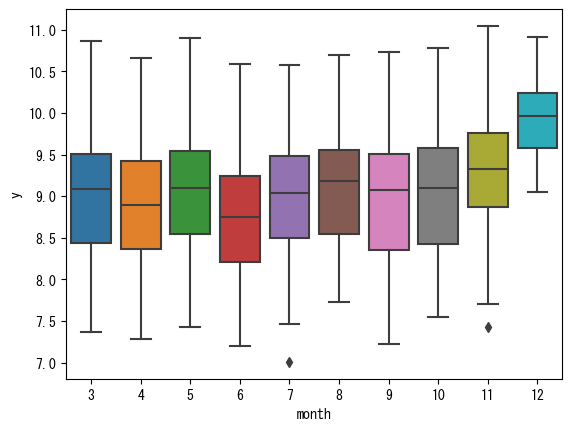

こちらは量的データではありますが、12月の観客数が多いというのはクライマックスに近いという点で関係がありそうです。このように量的データは相関が高くなくても有用な可能性はあるので要注意ですね。

# J1に絞ってチームごとに傾向を確認
data_J1 = train_df[train_df['stage'] == 'Ｊ１']
sns.boxplot(data=data_J1, x='home', y='y')
plt.xticks(rotation=90)
plt.show()

# J2に絞ってチームごとに傾向を確認
data_J2 = train_df[train_df['stage'] == 'Ｊ２']
sns.boxplot(data=data_J2, x='home', y='y')
plt.xticks(rotation=90)
plt.show()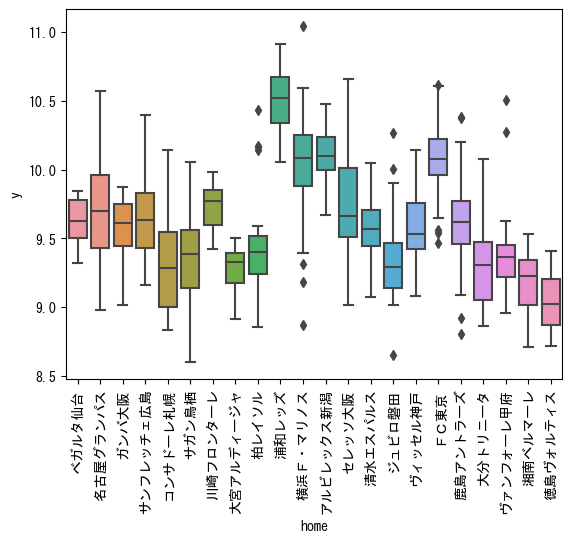

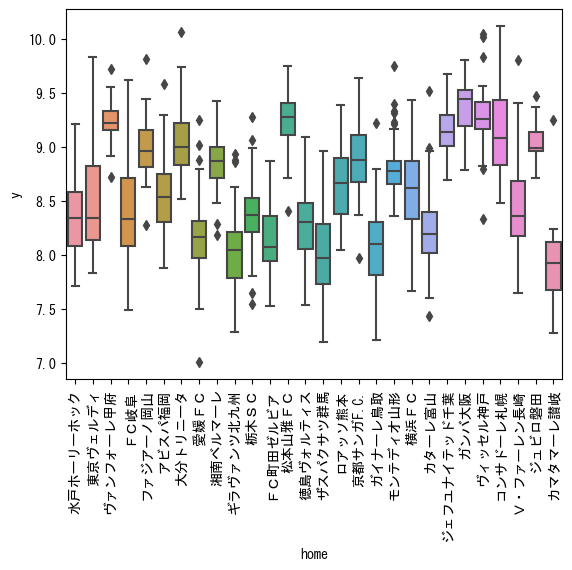
チームごとにも傾向は見られます。浦和レッズは昔からファンが多いイメージですがやはり観客数も多いですね。

同様にawayの試合も確認してみます。

# J1に絞ってチームごとに傾向を確認(away)
data_J1 = train_df[train_df['stage'] == 'Ｊ１']
sns.boxplot(data=data_J1, x='away', y='y')
plt.xticks(rotation=90)
plt.show()

# J2に絞ってチームごとに傾向を確認(away)
data_J2 = train_df[train_df['stage'] == 'Ｊ２']
sns.boxplot(data=data_J2, x='away', y='y')
plt.xticks(rotation=90)
plt.show()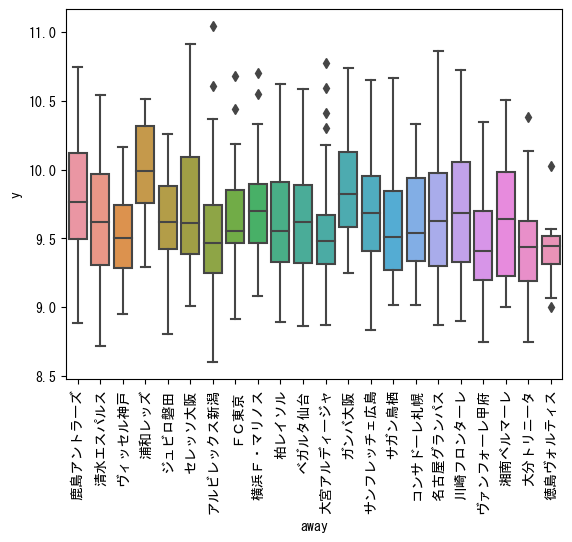

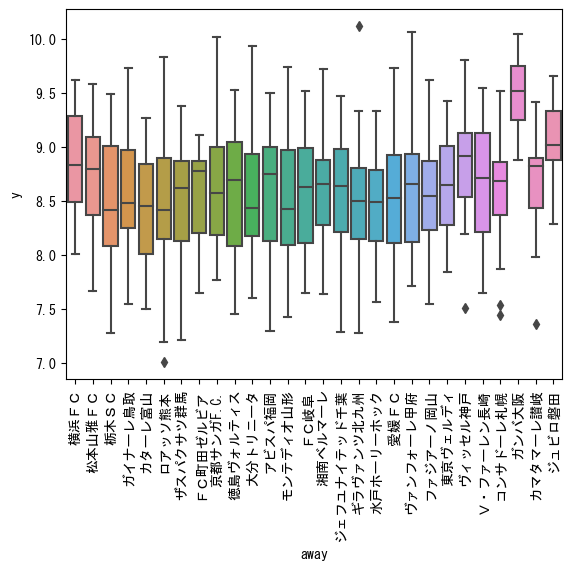
homeほど顕著ではありませんが、チームごとに傾向は見られます。

特徴量の選択・生成

特徴量の選択

これまで確認してきた結果より、yに影響を与えそうな特徴量は、capa, week, stage, month, home, awayであるため、まずこれらを抜き出してデータフレームを作り直します。

train_df_select = train_df[['capa', 'week', 'stage', 'month', 'home', 'away']]
test_df_select = test_df[['capa', 'week', 'stage', 'month', 'home', 'away']]

特徴量の生成

質的特徴量の確認の過程の中で、後で加工が必要そうだと考えていた2つの特徴量weatherとtvについて実際に加工してみます。

まず、天気については「晴れのち曇」だとか「曇時々雨」だとかパターンが多すぎるので、以下のようなコードでシンプルにまとめてしまいます。

def simplify_weather(weather):
    if '雪' in weather:
        return '雨'
    elif '雨' in weather:
        return '雨'
    elif '曇' in weather:
        return '曇'
    elif '晴' in weather:
        return '晴'
    else:
        return weather

train_df['weather_simple'] = train_df['weather'].apply(simplify_weather)
test_df['weather_simple'] = test_df['weather'].apply(simplify_weather)
print(train_df['weather_simple'].value_counts())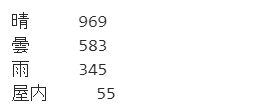

4種類にすっきりとまとまりました。その上でyとの関係を見てみます。

sns.boxplot(data=train_df, x='weather_simple', y='y') 
plt.show()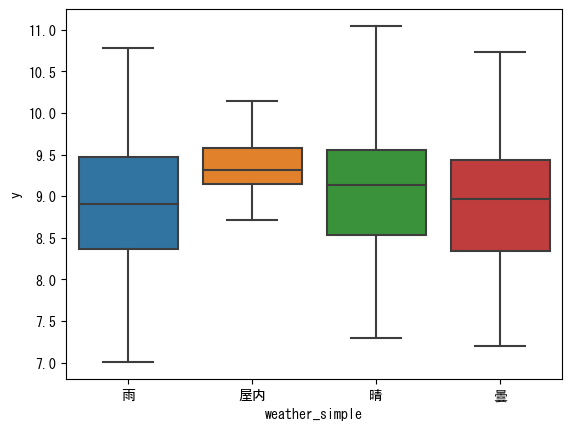

晴だと若干雨よりも観客数は多そうです。そして屋内は晴よりも安定して多い感じですね。

次にtvですが、これは各データに複数のテレビ局が含まれているため、その数をカウントしたカラムを作成してみます。

train_df['tv_num'] = train_df['tv'].apply(lambda x: len(x.split('／')))
test_df['tv_num'] = test_df['tv'].apply(lambda x: len(x.split('／')))

print(train_df['tv_num'].value_counts())

同様にyとの関係を見てみます。

sns.boxplot(data=train_df, x='tv_num', y='y') 
plt.show()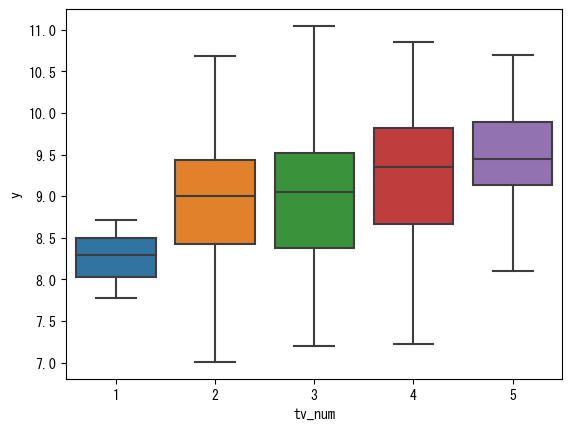

こちらはきれいな関係がありそうです。放送するテレビ局が多いほど注目されている試合ということで観客数も多いと考えると納得もいきます。

これらの新しく作成した特徴量も先ほどの特徴量に加えます。

train_df_select['weather_simple'] = train_df['weather_simple']
train_df_select['tv_num'] = train_df['tv_num']
test_df_select['weather_simple'] = test_df['weather_simple']
test_df_select['tv_num'] = test_df['tv_num']
print(train_df_select.columns)
print(test_df_select.columns)

次にこれらの質的データはそのままでは扱えないので、数値データに置き換えます。各特徴量について特に大小関係はありませんので、ここではダミー変数化を行います。

train_df_select = pd.get_dummies(train_df_select)
test_df_select = pd.get_dummies(test_df_select)
print(train_df_select.shape)
print(test_df_select.shape)

ダミー変数化によりカラム数が大幅に増えました。が、trainとtestでカラム数がずれてしまいましたので合わせる必要があります。

以下のようにtrainとtestを一度くっつけてからダミー変数を作成し、再度分けるという手順で対応しました。

# データセットを一時的に結合
n_train = len(train_df_select)
full_df = pd.concat([train_df_select, test_df_select])

# ダミー変数化
full_df = pd.get_dummies(full_df)

# 再度訓練データとテストデータに分割
train_df_select = full_df[:n_train]
test_df_select = full_df[n_train:]

print(train_df_select.shape)
print(test_df_select.shape)

今度はカラム数が一致しました。ちなみにダミー変数化によってどのようなカラムが増えたのかも見ておきます。

print(train_df_select.columns)

homeとawayで各チーム用のカラムができていることがカラム数が大きく増えた要因であることがわかります。

学習データと評価データの分割

さて、特徴量が決まりましたのでいよいよ学習用のデータの作成に入ります。

今回はsickit-learnのtrain_test_splitを使って分割を行います。

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(train_df_select, train_df['y'], random_state=0)
print(X_train.shape)
print(X_test.shape)
print(y_train.shape)
print(y_test.shape)

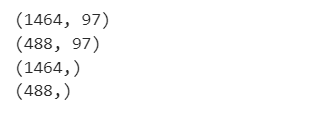
訓練データとテストデータが75:25に分割されていますね。

モデルの作成と学習(重回帰モデル)

そしていよいよ回帰モデルの学習です。ここではイメージがつかみやすい重回帰モデルを使用しますが、コードはいたってシンプル。以下の数行で学習してくれます。

from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(X_train, y_train)

出来上がったモデルの係数と切片を確認します。

coef_df = pd.DataFrame(lr.coef_, index=X_train.columns, columns=['Coefficients'])
pd.options.display.float_format = "{:.4f}".format # 表示を小数4桁まで
print(coef_df)
print('Intercept: ', lr.intercept_)

やはりcapaの影響が目立ちますね。

モデルの評価：RMSEによる予測精度の測定

予測精度の評価

作成したモデルで正しく予測ができるのか、まずは訓練データで試してみます。

y_pred_train = lr.predict(X_train)
print(y_pred_train)

予測は出来てそうです。ただし目的変数yについては最初に対数を取って正規化を行っているため、指数化して元に戻してあげる必要があります。

y_train_output = np.expm1(y_train) # 訓練データの目的変数yを指数化
y_pred_train_output = np.expm1(y_pred_train) # 訓練データの予測結果を指数化

その上でRMSEによる評価を行ってみます。

from sklearn.metrics import mean_squared_error as MSE

rmse_train = np.sqrt(MSE(y_train_output,y_pred_train_output))
print(rmse_train)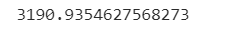

だいたい誤差が3000人ちょっとという結果になりました。同様にテストデータについても予測と評価を実施してみます。

y_pred_test = lr.predict(X_test)
y_test_output = np.expm1(y_test) # テストデータの目的変数yを指数化
y_pred_test_output = np.expm1(y_pred_test) # テストデータの予測結果を指数化

rmse_test = np.sqrt(MSE(y_test_output,y_pred_test_output))
print(rmse_test)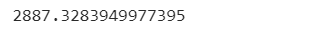

訓練データよりも結果がよくなりましたので、ひとまず過学習の心配なさそうです。

散布図で可視化してみます。

plt.scatter(y_test_output,y_pred_test_output)
# 範囲を決めるために最大値と最小値を取得
min_value = min(y_test_output.min(), y_pred_test_output.min())
max_value = max(y_test_output.max(), y_pred_test_output.max())
# 最小値・最小値から最大値・最大値への対角線を引く
plt.plot([min_value,max_value],[min_value,max_value])

plt.xlabel('実績値')
plt.ylabel('予測値')
plt.show()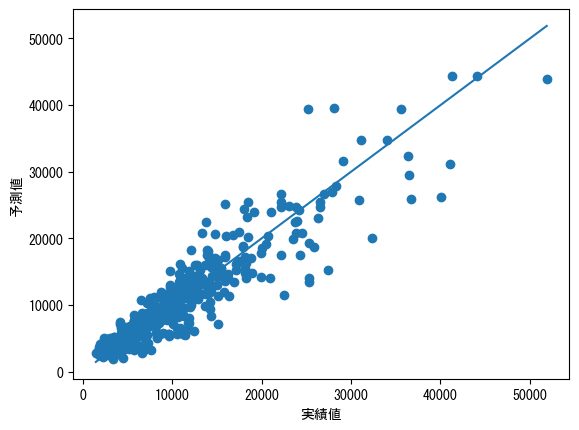

数値が大きい方が外れが大きく、特にRMSEによる評価だとこれらが響いてしまいますね。

モデルの改善を図りたいところですが、その前に提出データの予測も行い、どの程度の評価になるかを確認しておきます。

# test_df_selectの予測
predict = lr.predict(test_df_select)
predict_out = np.expm1(predict)

# 提出用フォーマットの読み込み
sample_df = pd.read_csv('sample_submit.csv', header=None)

# 予測結果をセットし保存
sample_df[1] = predict_out
sample_df.to_csv('output.csv', header=None, index=False)

作成したoutput.csvを提出します。そして結果は以下の通りでした。

自身の環境での予測よりも悪化してしまいました。

考えられる原因としては「この程度の差は普通に起こり得る」という可能性もありますし、あるいは提出データの機関である8月以降という部分の予想に弱い可能性もあります。

残差分析

ということでまずは大きく外れたデータに傾向がないか確認してみます。

まずは予測値と残差(実績値-予測値)の値を訓練とテストのデータフレームに追加します。

#  X_trainに予測値カラム(pred)を追加
X_train['pred'] = y_pred_train
# 実測値から予測値を引いた残差カラム
X_train['res'] = y_train - y_pred_train

# X_testに関しても同様にカラム追加
X_test['pred']  = y_pred_test
X_test['res'] = y_test - y_pred_test

次に訓練とテストのデータフレームを縦につなげ、元のtrain_dfと結合してどのようなデータに残差が多いのかの確認を試みます。

tmp = pd.concat([X_train, X_test])
train_df_check =  pd.concat([train_df, tmp[['pred', 'res']]], axis=1)

# 残差が大きい順に20個表示
x = train_df_check.sort_values(by = 'res', ascending = False )

x.head(20)

ここでは出力結果は省略しますが、共通点として読み取れた内容は以下の通りです。

• ステージ(stage)：J2の試合が大半
• テレビ放送(tv)：「スカパー！／スカパー！プレミアムサービス」が放送した試合が半数以上
• 曜日(week)：日曜日の試合が半数以上

真ん中の要因についてはもともと「スカパー！／スカパー！プレミアムサービス」が圧倒的に多いので当然の結果として、残りの2つについて何か改善ができないか考えてみます。

モデルの改善

さて、これらの結果などを踏まえてモデルの改善を考えてみます。

月の特徴量を加工

このモデルでは’month’をそのまま使用していますが、月の数字に対して観客数が比例しているというわけではなく特定の月に上昇が見られるだけというのが実態です。よってこれを加工することで特に提出データの期間である年後半部分の改善を狙ってみます。

まず、月と観客数の関係を再掲します。

これを見ると6月は観客数がやや少なく、11月は少し多く、12月が際立って多く見えます。その要因を探るためにJ1とJ2に分けて見てみます。

# stageがJ1のデータ。
sns.boxplot(data=train_df[train_df['stage'] == 'Ｊ１'], x='month', y='y')
# 可視化結果を表示する為に必要な関数
plt.show()

# stageがJ2のデータ
sns.boxplot(data=train_df[train_df['stage'] == 'Ｊ２'], x='month', y='y')
# 可視化結果を表示する為に必要な関数
plt.show()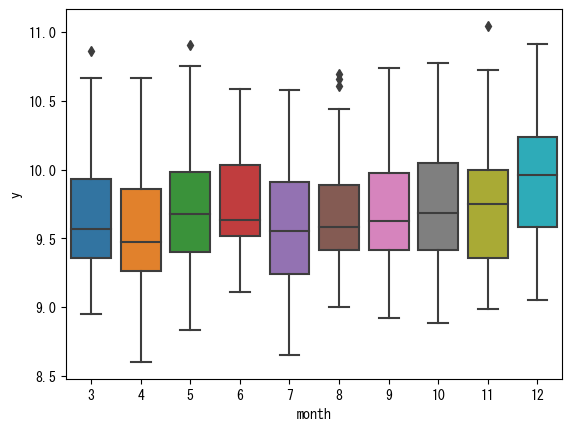

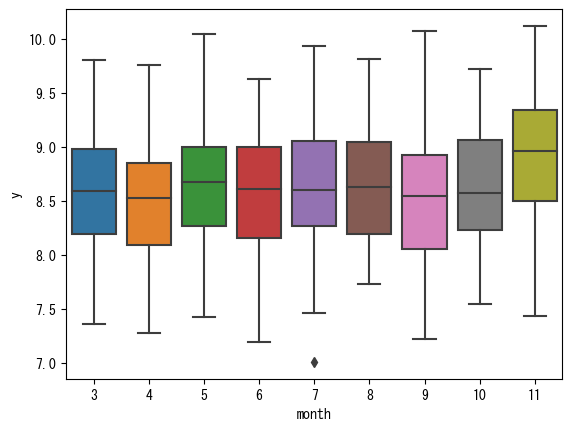
まず6月の少なさが目立たなくなりました。これはどういうからくりかというと、6月はJ1の試合数がかなり少なく、そのためJ2の割合が大きくなります。J2はJ1に比べて観客数が少ないため、全体で見ると低く見えたわけです。よって6月は加工不要と考えます。

J1とJ2の各月の試合数の確認結果も載せておきます。

J1_counts = data_J1['month'].value_counts().sort_index()
J2_counts = data_J2['month'].value_counts().sort_index()

# Combine the two Series into a DataFrame
month_counts = pd.DataFrame({
    'J1': J1_counts,
    'J2': J2_counts
})

month_counts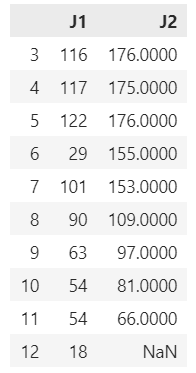

ご覧の通り6月のJ1の試合数はかなり少なくなっています。

また、箱ひげ図によると年の終盤にかけて観客数が多くなってきますが、J1は12月まで試合があるので11月にやや上昇して12月に大きく上昇、J2は11月に終わるので11月に大きく観客数が上昇していると考えられます。

その他の月には大きな特徴がありませんので、上記に当てはまるデータだけを特徴量としてピックアップして、month列は消してしまおうと思います。

train_df_select['J1_Nov'] = ((train_df_select['stage'] == 'Ｊ１') & (train_df_select['month'] == 11)).astype(int)
train_df_select['J1_Dec'] = ((train_df_select['stage'] == 'Ｊ１') & (train_df_select['month'] == 12)).astype(int)
train_df_select['J2_Nov'] = ((train_df_select['stage'] == 'Ｊ２') & (train_df_select['month'] == 11)).astype(int)
test_df_select['J1_Nov'] = ((test_df_select['stage'] == 'Ｊ１') & (test_df_select['month'] == 11)).astype(int)
test_df_select['J1_Dec'] = ((test_df_select['stage'] == 'Ｊ１') & (test_df_select['month'] == 12)).astype(int)
test_df_select['J2_Nov'] = ((test_df_select['stage'] == 'Ｊ２') & (test_df_select['month'] == 11)).astype(int)
train_df_select = train_df_select.drop(columns='month')
test_df_select = test_df_select.drop(columns='month')

このデータを基に再度学習から検証までを行います。

# データセットを一時的に結合
n_train = len(train_df_select)
full_df = pd.concat([train_df_select, test_df_select])

# ダミー変数化
full_df = pd.get_dummies(full_df, drop_first=True)

# 再度学習用データと提出用データに分割
train_df_select = full_df[:n_train]
test_df_select = full_df[n_train:]

# 学習用データを訓練データとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(train_df_select, train_df['y'], random_state=0)

# 線形モデルで学習
lr = LinearRegression()
lr.fit(X_train, y_train)

# 訓練データの予測
y_pred_train = lr.predict(X_train)
y_train_output = np.expm1(y_train) # 訓練データの目的変数yを指数化
y_pred_train_output = np.expm1(y_pred_train) # 訓練データの予測結果を指数化

# テストデータの予測
y_pred_test = lr.predict(X_test)
y_test_output = np.expm1(y_test) # テストデータの目的変数yを指数化
y_pred_test_output = np.expm1(y_pred_test) # テストデータの予測結果を指数化

# RMSEで評価
rmse_train = np.sqrt(MSE(y_train_output,y_pred_train_output))
rmse_test = np.sqrt(MSE(y_test_output,y_pred_test_output))
print("rmse_train : " + str(rmse_train))
print("rmse_test : " + str(rmse_test))

# 散布図の作成
plt.scatter(y_test_output,y_pred_test_output)
min_value = min(y_test_output.min(), y_pred_test_output.min())
max_value = max(y_test_output.max(), y_pred_test_output.max())
plt.plot([min_value,max_value],[min_value,max_value])

plt.xlabel('実績値')
plt.ylabel('予測値')
plt.show()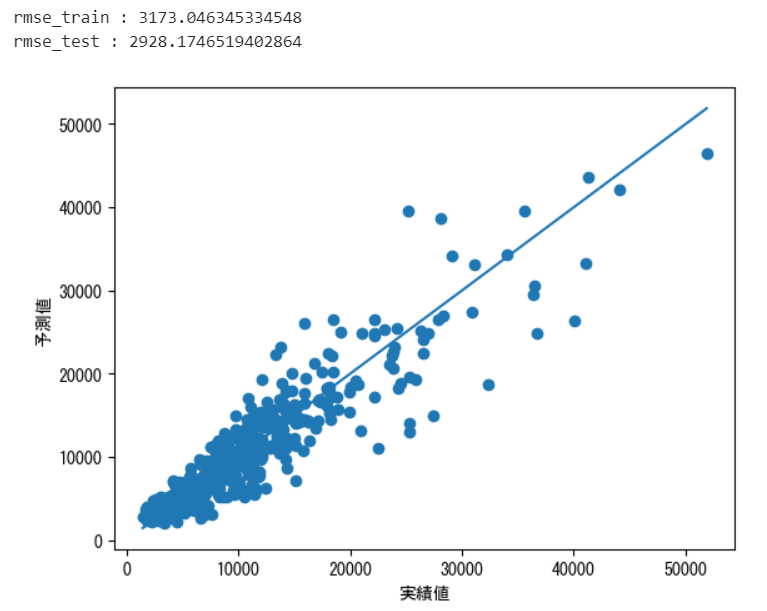

RMSEにはあまり大きな変化は見られませんが、どちらかというと年後半のデータに効くはずなので、提出用データの改善に期待してデータの提出まで行ってみます。

改善前が3662.7だったので、ある程度の改善効果が得られました。

その他の特徴量の工夫

このあと、以下のようなことを試したのですが成績向上にはつながりませんでした。

• 日曜日の乖離が大きかったことから、土曜日曜とそれ以外という形でデータを作成
• J1とJ2で曜日のずれ方が違ったことから、stage+weekという新たな特徴量の作成

工夫したからといって必ずしも成果に結びつくわけではないところが、辛いところでもありまたやりがいもあるところですよね。

機械学習モデルの変更

「まずはLightGBMを試してみるべし」というくらいテーブルデータの分析においてLightGBMは強力なアルゴリズムです。

そこで適当なグリッドサーチをかけつつ、LightGBMで学習させてみました。変更部分のコードは以下になります。

from sklearn.model_selection import GridSearchCV
from lightgbm import LGBMRegressor

# Initialize the LightGBM model
lgbm = LGBMRegressor(random_state=0)

# Define the parameter grid
param_grid = {
    'n_estimators': [300, 500, 1000, 3000, 5000, 7000],
    'learning_rate': [0.01, 0.1, 0.3,  0.5, 0.7],
    'max_depth': [2, 3, 5]
}

# Create a GridSearch object
grid_search = GridSearchCV(estimator=lgbm, param_grid=param_grid, cv=5, scoring='neg_mean_squared_error')

# Fit the GridSearch to our training data
grid_search.fit(X_train, y_train)

# Get the best parameters
best_params = grid_search.best_params_

print("Best parameters: ", best_params)

# Train and evaluate the model with the best parameters
lgbm_best = LGBMRegressor(**best_params)
lgbm_best.fit(X_train, y_train)

# 訓練データの予測
y_pred_train = lgbm_best.predict(X_train)
y_train_output = np.expm1(y_train) # 訓練データの目的変数yを指数化
y_pred_train_output = np.expm1(y_pred_train) # 訓練データの予測結果を指数化

# テストデータの予測
y_pred_test = lgbm_best.predict(X_test)
y_test_output = np.expm1(y_test) # テストデータの目的変数yを指数化
y_pred_test_output = np.expm1(y_pred_test) # テストデータの予測結果を指数化

このモデルで予測した結果を提出したところ…

ほんのわずかですが改善しました。いや、正直もっと改善するかと思っていたのですがそれほどでもなかったですね。LightGBMといえど万能ではないようです。

さらなる改善の可能性

この時点で投稿者数2005人に対してランキングは460位。上位25%に入れたので及第点としてこのコンペは終了したいと思います。

なお、今後これを対応すれば大きく改善するだろうと考えたのは、特徴量として「試合開始前時点の順位」を追加することです。これは外部データとしてどこかから引っ張ってきてもいいですし、それまでの成績を元に計算することもできるはずです。

例えば優勝争いをしているチームの方が下位チームよりも観客数は多いと想定されますので、さらなる上位を狙うのであれば試してみたいところですが、時間がかかりそうなので今回はやりません笑

以上、【練習問題】Jリーグの観客動員数予測についてのチャレンジ内容でした。このコンペに今後練習問題として取り組む方の参考になれば幸いです。この記事を真似するだけでも上位25%には入れますのであなた自身の工夫と組み合わせてさらなる上位を目指してみて下さい。