SIGNATEの学習コースQuest「金融機関におけるテレマーケティングの効率化」の総仕上げとして、コンペの練習問題「銀行の顧客ターゲティング」に取り組みました。
コンペの概要
実際のビジネス環境で得られたデータを用いて、マーケティングキャンペーンの効率化を目指すモデルを構築します。データセットは、ある銀行の顧客属性データと過去のキャンペーン接触情報から成り、これを基にキャンペーン結果(口座開設の有無)を予測します。学習用データは27,168名の顧客データ、予測対象は18,083名のキャンペーン反応です。
入力データは以下です。
| カラム | ヘッダ名称 | データ型 | 説明 |
|---|---|---|---|
| 0 | id | int | 行の通し番号 |
| 1 | age | int | 年齢 |
| 2 | job | varchar | 職種 |
| 3 | marital | varchar | 未婚/既婚 |
| 4 | education | varchar | 教育水準 |
| 5 | default | varchar | 債務不履行があるか(yes, no) |
| 6 | balance | int | 年間平均残高(€) |
| 7 | housing | varchar | 住宅ローン(yes, no) |
| 8 | loan | varchar | 個人ローン(yes, no) |
| 9 | contact | varchar | 連絡方法 |
| 10 | day | int | 最終接触日 |
| 11 | month | char | 最終接触月 |
| 12 | duration | int | 最終接触時間(秒) |
| 13 | compaign | int | 現キャンペーンにおける接触回数 |
| 14 | pdays | int | 経過日数:前キャンペーン接触後の日数 |
| 15 | previous | int | 接触実績:現キャンペーン以前までに顧客に接触した回数 |
| 16 | poutcome | varchar | 前回のキャンペーンの成果 |
| 17 | y | boolean | 定額預金申し込み有無(1:有り, 0:無し) |
コンペの詳細は以下のページをご覧ください。
https://signate.jp/competitions/1
まずはQuestで学習した内容に沿ってモデルの構築を行っていきます。
大まかな流れについては別途まとめましたので以下の記事を参考にしてください。
この記事で学べること 機械学習の二値分類の基本概念と実装方法 Pythonとscikit-learnを使った実践的なコーディング データ前処理から評価まで一連の流れ 複数の分類手法の比較と選び方 実務で使える評価指標の使い分け 対[…]
データの確認と理解
まずはデータの中身を確認します。
基本統計量の確認
# 必要なライブラリのインポート
import pandas as pd
# データの読み込み
data = pd.read_csv('train.csv', index_col='id')
data.describe()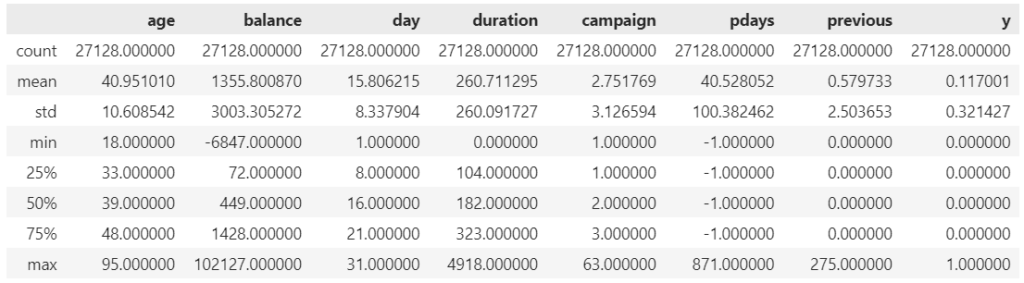
balance(年間平均残高)の平均値と中央値が乖離しているので、一部の人たちの残高が平均を大きく引き上げていそうです。
オブジェクト型の特徴量についても同様に見ておきます。
data.describe(include=['O'])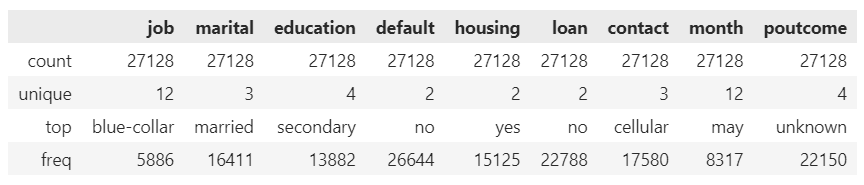
default(債務不履行があるか)がほぼnoであること、poutcome(前回のキャンペーンの成果)の大半がunknownであることなどが気になるところですかね。
poutcomeはデータの種類と数も見ておきましょうか。
data['poutcome'].value_counts()
前回のキャンペーンの結果は参考になるかもしれませんね。
データの可視化と相関の確認
先にオブジェクト型の特徴量とyの関係を見ておきます。以下のコードで各カテゴリごとにy=1の占める比率を棒グラフ化します。
import matplotlib.pyplot as plt
# カラム名のリストを作成
columns = ['job', 'marital', 'education', 'default', 'housing', 'loan', 'contact', 'month', 'poutcome']
# 各カラムについてループを回す
for column in columns:
# pd.crosstabを使ってカラムと'y'の関係を計算
cross_tab = pd.crosstab(df[column], df['y'], normalize='index')
# 比率を棒グラフで表示
cross_tab.plot(kind='bar', stacked=True, figsize=(10, 5))
# グラフのタイトルを設定
plt.title(f"Proportion of y=1 in each category of {column}")
# グラフを表示
plt.show()
順に見ていきます。
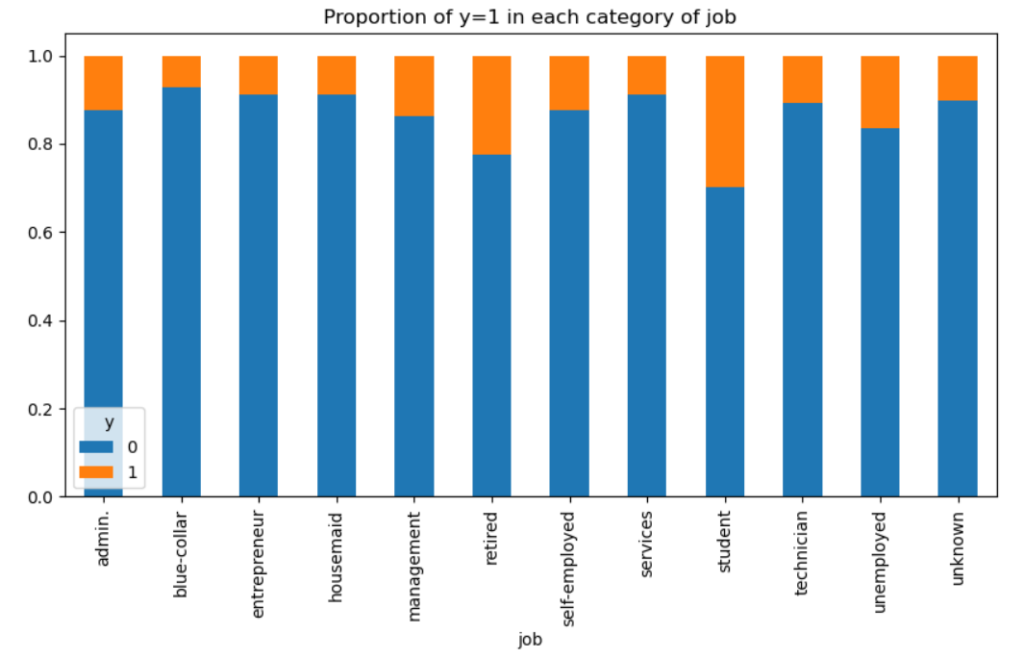
職業別では、retiredとstudentの2つが他よりもy=1(口座開設)の比率が高いですね。お年寄りは説得されると乗ってしまうイメージがありますが、studentは意外でした。
この結果から、銀行がマーケティングキャンペーンを計画する際にはこれらの顧客層に焦点を当てる必要があるという可能性を示しています。
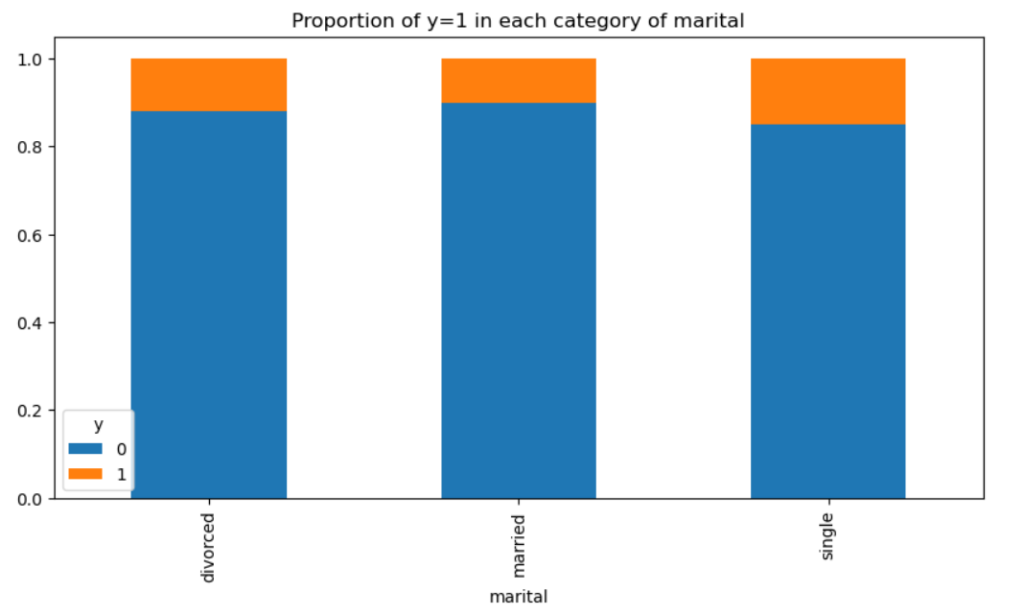
婚姻状況とは関係ないようです。
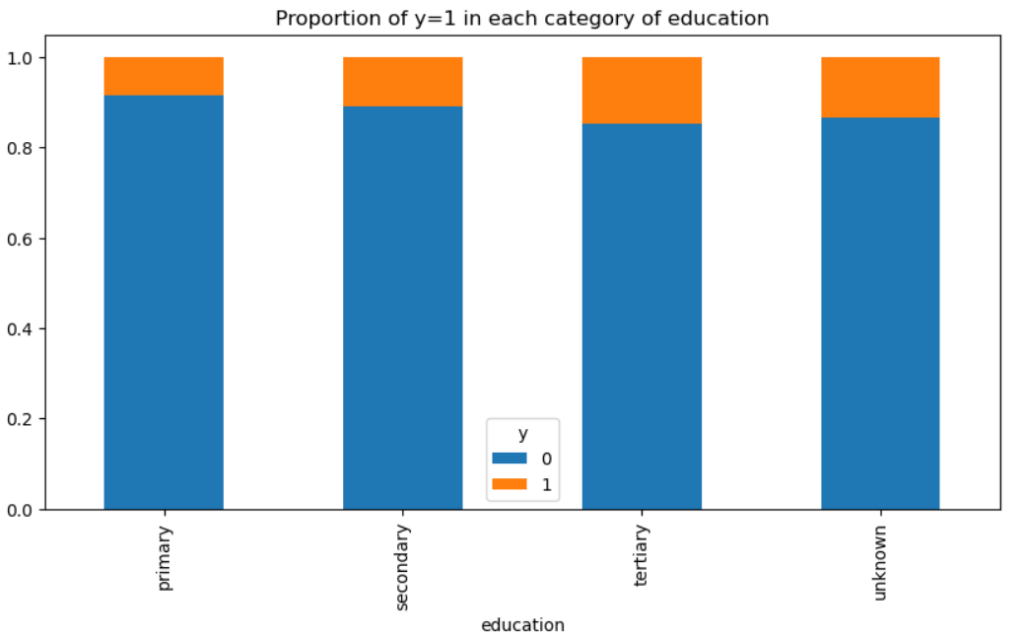
差があるか微妙なところですが、教育レベルが高い方がやや口座開設率は高そうです。
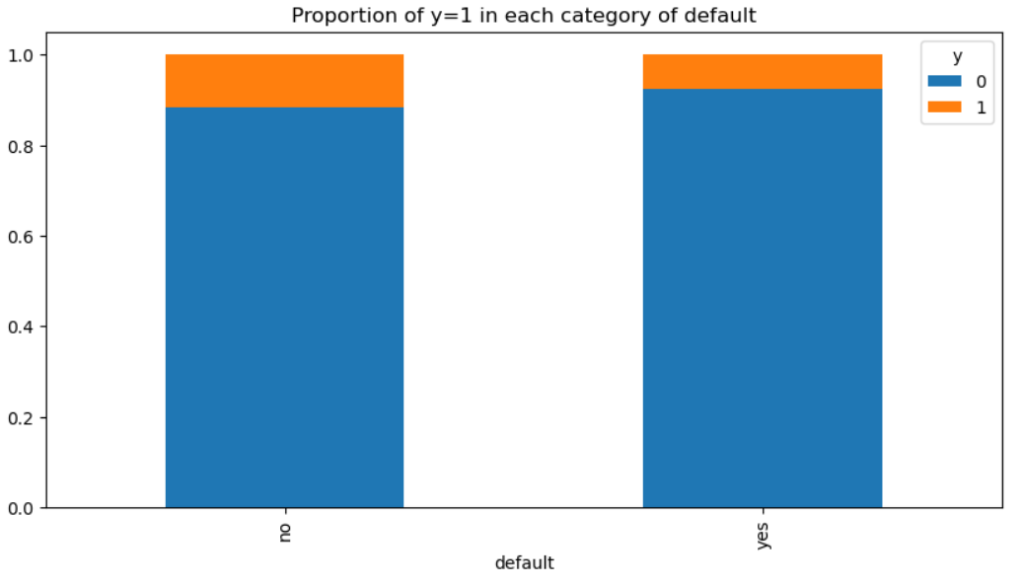
債務不履行がない人の方が口座開設する可能性がやや高いようですね。
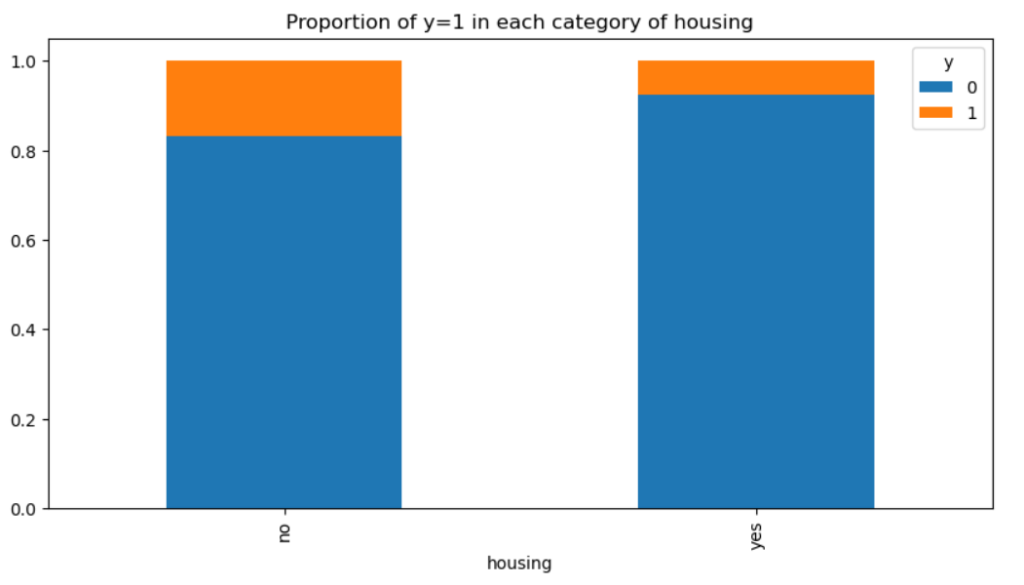
住宅ローンについては借りていない人の方が口座開設の可能性高そうです。
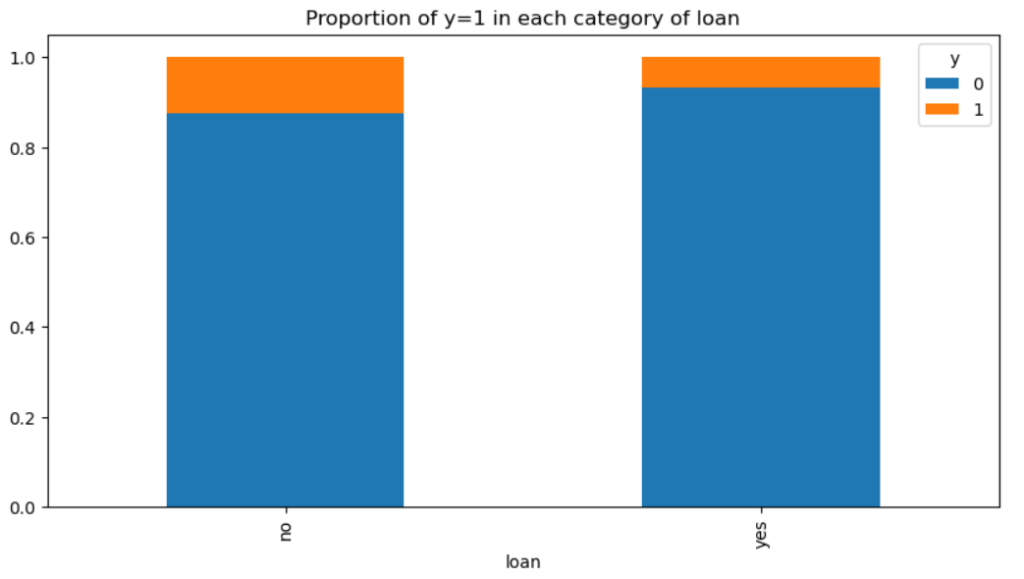
個人ローンも同様です。
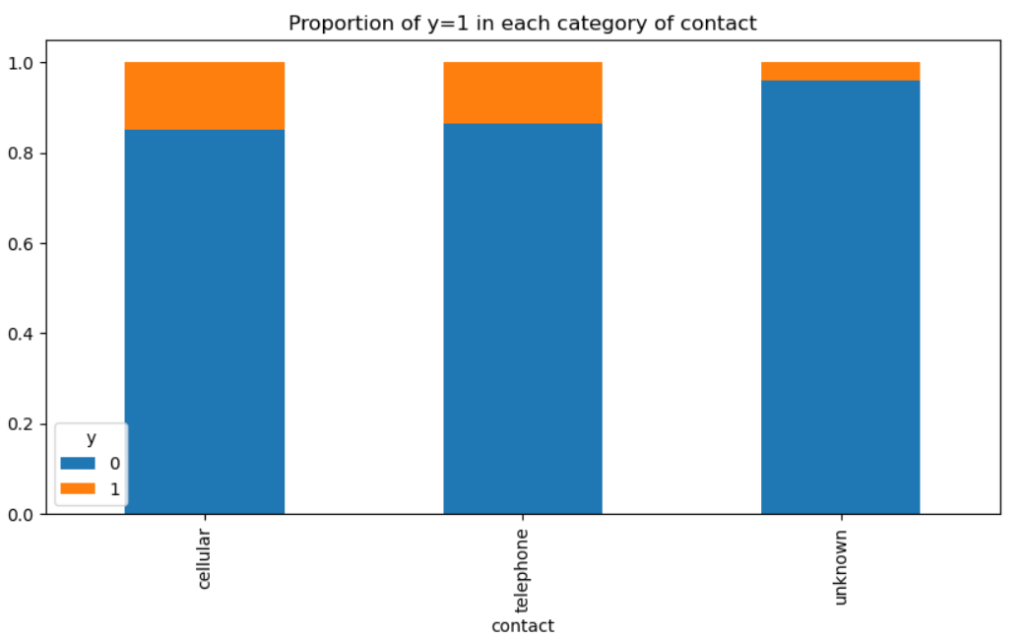
連絡手段として携帯電話・普通の電話を使うと成功率が高いようです。
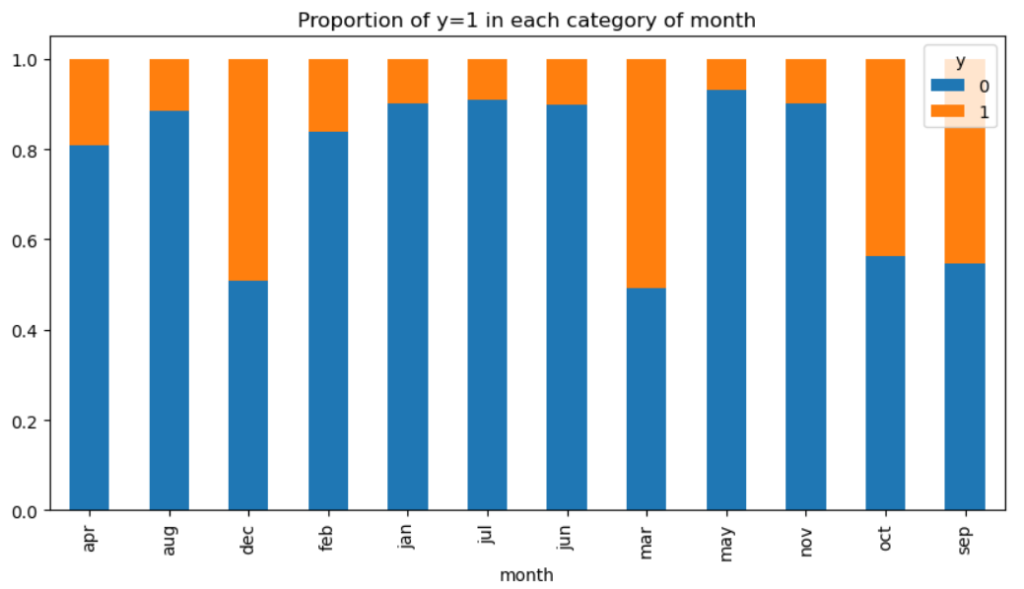
特定の月に成功率が高いというのは違和感がありますが、これはキャンペーンをやっている月などの可能性もありますね。その場合は月との本質的な因果関係はないのでこの特徴量は使用しない方が無難かもしれません。
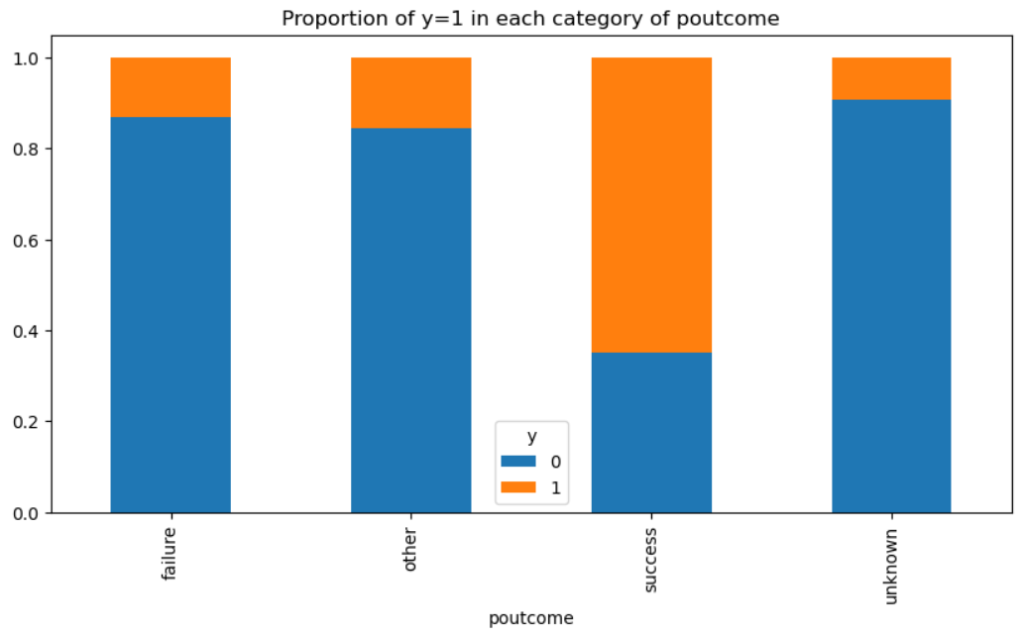
基本統計量の確認でも気になっていたこの「前回のキャンペーンの成果」ですが、前回成功している人は明らかに今回の成功率も高いですね。前回失敗やその他の成功率もunknownより高い点は気になりますが、基本統計量の確認でunknownがデータの大半であったことと併せて考えると、「前回の結果がわかるくらい接触回数が多い人は成功しやすい」と見ることができるかもしれません。
次に定量データの相関係数を確認します。
# データフレームの各列間の相関係数を計算
corr_matrix = df.corr()
# seabornのheatmap関数を使用して、相関行列を視覚化
sns.heatmap(corr_matrix, cmap="Reds")
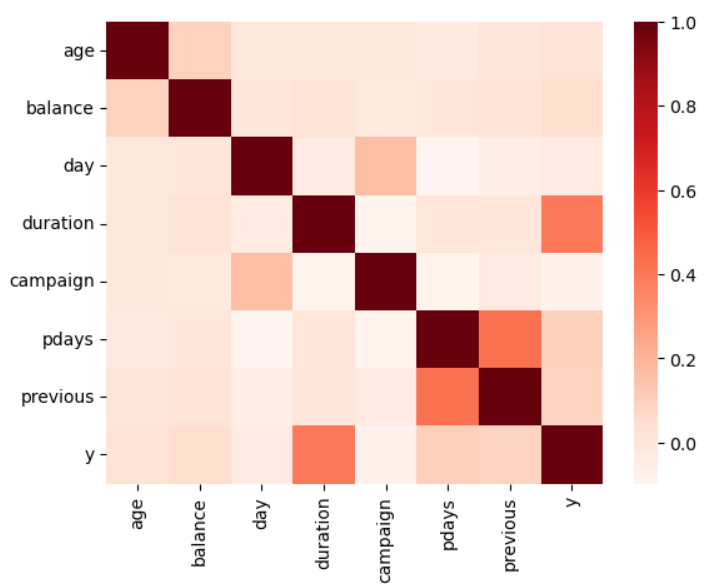
yと相関が高いのはduration(最終接触時間(秒))です。お客さんとの接触時間が長いほど申し込み数が多いというのはわかりやすいですね。
その他はprevious(現キャンペーン以前までに顧客に接触した回数)とpdays(前キャンペーン接触後の日数)の間で相関が高いことがわかります。
durationとyの相関が大きいことがわかったため、yが0の場合と1の場合で分けてduratonとの関係をヒストグラムで見てみます。
# 必要なライブラリのインポート
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
# データの読み込み
data = pd.read_csv('train.csv', index_col='id')
# 'y'の値によって'duration'のデータを分割
duration_when_y_is_0 = data[data['y']==0]['duration']
duration_when_y_is_1 = data[data['y']==1]['duration']
# ヒストグラムの作成
sns.distplot(duration_when_y_is_0, label='y=0')
sns.distplot(duration_when_y_is_1, label='y=1')
# グラフのタイトル、軸ラベルの設定
plt.title('Duration Histogram')
plt.xlabel('Duration')
plt.ylabel('Frequency')
# x軸の表示範囲の指定
plt.xlim(0, 2000)
# グラフの凡例を追加
plt.legend()
# グラフの表示
plt.show()
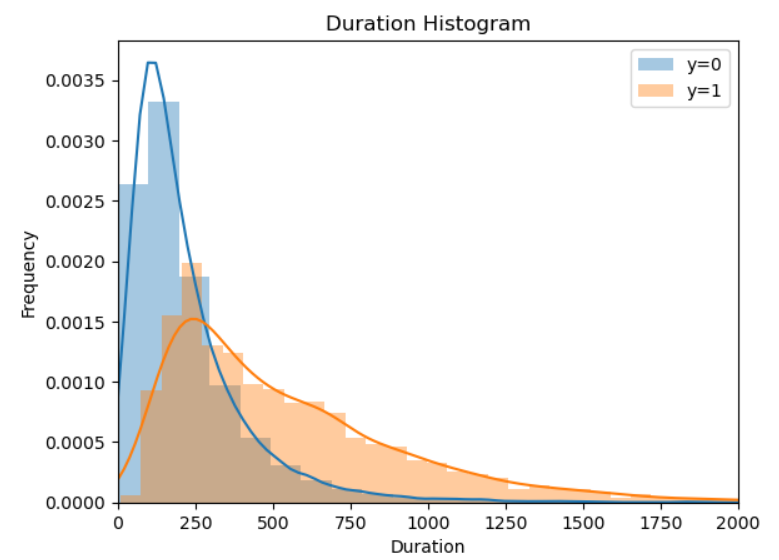
グラフにしてみるとよくわかりますね。明らかにDration(接触時間)が多い方が成約につながりそうです。
調べようと思えばまだまだ調べられそうですが、練習問題なのでひとまずデータの確認はこれくらいにしておきます。
特徴量の選択と前処理
さて、ここで上で確認した内容に従って特徴量を絞り込んでもいいのですが、学習したQuestではすべての特徴量を使用していたので、それに従ってここでも絞り込みは行わずに行こうと思います。
前処理についてもget_dummies関数をデータフレームにそのまま適用していたので、同様に対応します。
# pandasのインポート
import pandas as pd
# データの読み込み
df = pd.read_csv('train.csv', index_col='id')
# データの列数の表示
print( df.shape[1] )
# ダミー変数化
df = pd.get_dummies(df)
# ダミー変数化後のデータの列数の表示
print( df.shape[1] )
列数は17から52に増えましたが、これくらいのデータ数であれば難なく学習できるでしょう。簡単ですが、欠損値もありませんでしたので今回の前処理はこれで終わります。
モデルの作成と学習
さて、いよいよモデルの作成に入りますが、まずは学習用データの作成からです。
目的変数と特徴量
まずは目的変数yとそれ以外の説明変数(特徴量)Xに分けます。
# data_yに目的変数を代入
data_y = df['y']
# data_Xに説明変数を代入
data_X = df.drop('y', axis=1)学習データと評価データの分割
次に、train_test_split関数にて学習用データと評価用データに分けますが、今回は8:2の比率で分割します。
# train_test_splitのインポート
from sklearn.model_selection import train_test_split
# 学習データと評価データにデータを分割
train_X, test_X, train_y, test_y = train_test_split(data_X, data_y, test_size=0.2, random_state=0)モデルの選択と学習
今回はQuestで学んだ決定木を使用します。ランダムフォレストや勾配ブースティングなどの決定木の派生形モデルは何度も使ったことがありますが、オリジナルを使うのは初めてでした。
パラメーターも同様に木の深さ2で試してみます。
# 決定木モデルのインポート
from sklearn.tree import DecisionTreeClassifier as DT
# 決定木モデルの準備
tree = DT(max_depth = 2, random_state = 0 )
# 決定木モデルの学習
tree.fit(train_X, train_y)続いてどの特徴量が使われたか、重要度を出力してみましょう。
# 重要度に名前を付けて降順に表示
importance = pd.Series(tree.feature_importances_, index=train_X.columns)
importance_sorted = importance.sort_values(ascending=False)
print(importance_sorted)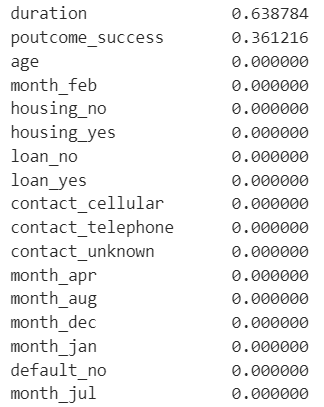
途中までの出力ですが、duration(最終接触時間)とpoutcome_success(前回のキャンペーンの結果)だけが使われていますね。深さを2としているので特徴量の数が限られるのは仕方ありません。この2つはデータの確認にの際に影響がありそうな特徴量だったので、違和感もありません。
これでモデルの学習は終わりましたので、このモデルを使って検証データを予測します。
# 評価用データの予測
pred_y1 = tree.predict_proba(test_X)[:,1]モデルの評価
さて、予測が終わったらその評価です。この課題の最終評価方法でもあるAUCを用います。
from sklearn.metrics import roc_auc_score
# 評価用データの予測
pred_y1 = tree.predict_proba(test_X)[:,1]
# 実測値test_y,予測値pred_y1を使ってAUCを計算
auc1=roc_auc_score(test_y,pred_y1)
# 評価結果の表示
print(auc1)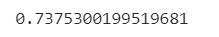
約0.74という数字が出ました。これはQuestの同じパラメータでの結果ともほぼ合致します。
ROCも描画してみます。
from sklearn.metrics import roc_curve
import matplotlib.pyplot as plt
# 実測値test_yと予測値pred_y1を使って偽陽性率、真陽性率、閾値の計算
fpr, tpr, thresholds = roc_curve(test_y, pred_y1)
# ラベル名の作成
roc_label = 'ROC(AUC={:.2}, max_depth=2)'.format(auc1)
# ROC曲線の作成
plt.plot(fpr, tpr, label=roc_label)
# 対角線の作成, グラフにタイトルを追加, グラフのx軸とy軸に名前を追加, x軸とy軸の表示範囲の指定
plt.plot([0, 1], [0, 1], color='black', linestyle='dashed')
plt.title('ROC')
plt.xlabel('FPR')
plt.ylabel('TPR')
plt.xlim(0, 1)
plt.ylim(0, 1)
# 凡例の表示とグラフの表示
plt.legend()
plt.show()
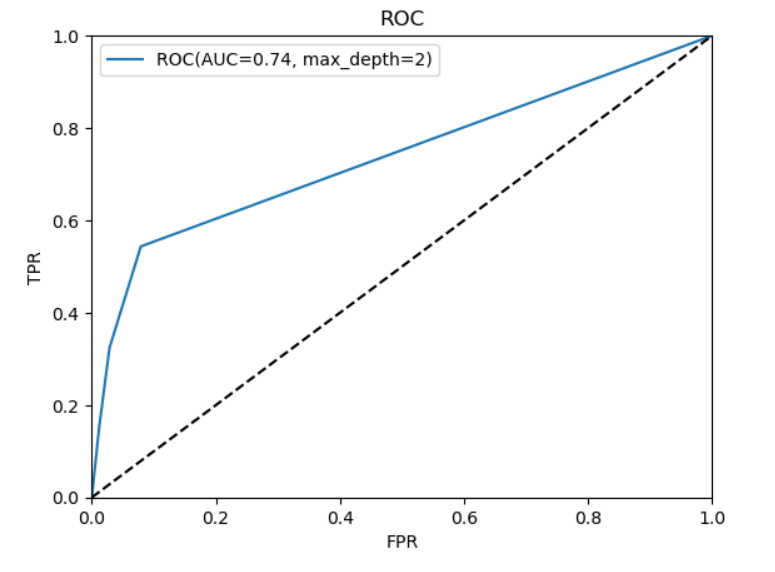
それっぽい図が完成しました。
また、せっかく深さが小さくて分岐が見やすいので、ツリー構造も見てみます。
# 決定木描画ライブラリのインポート
from sklearn.tree import export_graphviz
# 決定木グラフの出力
export_graphviz(tree, out_file="tree.dot", feature_names=train_X.columns, class_names=["0","1"], filled=True, rounded=True)
# 決定木グラフの表示
from matplotlib import pyplot as plt
from PIL import Image
import pydotplus
import io
g = pydotplus.graph_from_dot_file(path="tree.dot")
gg = g.create_png()
img = io.BytesIO(gg)
img2 = Image.open(img)
plt.figure(figsize=(img2.width/100, img2.height/100), dpi=100)
plt.imshow(img2)
plt.axis("off")
plt.show()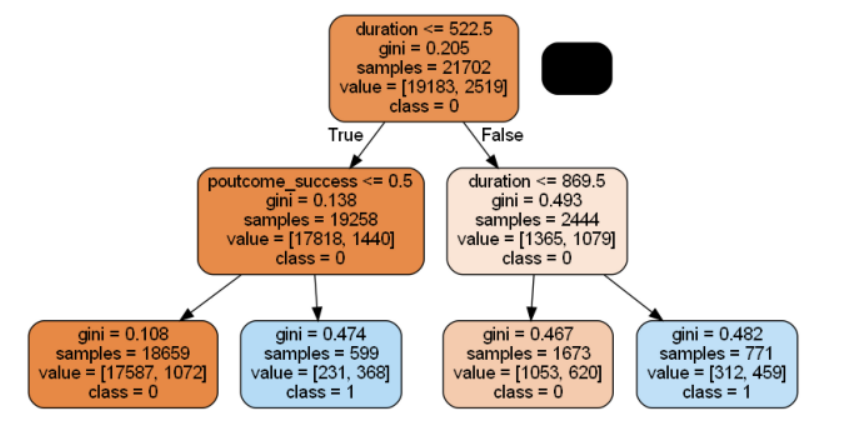
深さ2なので、duration(最終接触時間)とpoutcome_success(前回のキャンペーンの結果)しか使われていないことがよくわかりますね。
そして末端の要素を見るとclass1と分類されていても(2番目と4番目)、その中身(value)にはかなりclass0の要素が入ってしまい、ジニ係数も高いです。
これはまだまだ改善の余地がありそうですね。なお、ツリーの描画については別途記事にしているので、そちらもご参考にしてください。
「決定木」は機械学習のアルゴリズムの一つで、その名の通り木のような構造を持つモデルです。この記事では、決定木の視覚化について解説します。視覚化は、モデルの動作を理解し結果を解釈するための強力なツールですのでぜひご参考にしてください。 […]
データの提出とスコア確認
さて、先ほどのスコア0.74は自ら作成した検証用データを予測したスコアなので、提出用のテストデータ(test.csv)についても予測して、実際に提出してみます。
まずはそのためのコードを書きます。
# テストデータの読み込み
input_df = pd.read_csv('test.csv', index_col='id')
# ダミー変数化
df = pd.get_dummies(input_df)
# テストデータの予測
pred_y2 = tree.predict_proba(df)[:,1]
# sampleファイルを読み込んで予測結果で上書き
output_df = pd.read_csv('submit_sample.csv', header=None)
output_df[1] = pred_y2
output_df.to_csv('output.csv', header=None,index=False)
提出するとほどなくしてスコアが送られてきますが、結果は以下の通りでした。

自分の評価データで計算したスコアとほとんど同じでした。
モデルの改善
さて、当然ですが一度提出して終わりではありません。練習問題といえどある程度の改善はしてみたいですよね。
こちらの練習問題ではチュートリアルを書いてくれてる方がいて、この方のスコアが0.7985ということなので、せめてこれより上は目指したいです(同じスコアであれば丸々コピーすれば達成できてしまうので)。
自分で整理した記事によると、改善のためには大きく以下3つの方法があるとのことなので、これを参考にしてみます。
- データを増やす
- アルゴリズムの変更・チューニング
- 特徴量を増やす・減らす
このうちまずは効果の高そうなアルゴリズムの変更・チューニングをしてみます。
グリッドサーチによるパラメータの改善
さて、まずはQuestで学んだ内容に従って、グリッドサーチを使ってモデルの最適なパラメータを探してみたいと思います。
なお、グリッドサーチの手順についてはこちらの記事もご参照ください。
機械学習モデルの性能を最大化するために欠かせないのがGridSearchCV(グリッドサーチ)を使ったハイパーパラメータの最適化です。 本記事では、PythonのsciKit-learnライブラリを使って、GridSearchCVの使い[…]
ここでは最適なmax_depthを探るべく、2~10まで試してみます。
# 必要なライブラリをインポート
from sklearn.tree import DecisionTreeClassifier as DT # 決定木モデルを使用するためのライブラリ
from sklearn.model_selection import GridSearchCV # モデルのパラメータ探索を行うためのグリッドサーチのライブラリ
# 決定木モデルを準備
tree = DT(random_state=0)
# グリッドサーチで探索するパラメータを設定
# ここでは、決定木の深さ(max_depth)を2から10まで探索
parameters = {'max_depth':[2,3,4,5,6,7,8,9,10]}
### グリッドサーチの設定
# 探索対象のモデル(tree)、探索パラメータ(parameters)、交差検証(cv)の分割数を5、
# return_train_scoreをTrueに設定して、トレーニングデータでのスコアも返すように設定
gcv = GridSearchCV(tree, parameters, cv=5, scoring='roc_auc', return_train_score=True)
# グリッドサーチを実行。
# この処理により、最適なパラメータが自動的に選択され、そのパラメータを使用したモデルが学習される。
gcv.fit(train_X, train_y)
トレーニングデータのスコアを元に学習の様子をプロットさせてみます。
# ライブラリをインポート
from matplotlib import pyplot as plt
# グリッドサーチの結果から、トレーニングスコアとテストスコアを取得
train_score = gcv.cv_results_["mean_train_score"]
test_score = gcv.cv_results_["mean_test_score"]
# 探索パラメータのリスト
params = [2,3,4,5,6,7,8,9,10]
# トレーニングスコアとテストスコアをプロット
plt.plot(params, train_score, label="train_score")
plt.plot(params, test_score, label="test_score")
# グラフの設定
plt.title("train_score vs test_score") # タイトル
plt.xlabel("max_depth") # x軸ラベル
plt.ylabel("AUC") # y軸ラベル
plt.legend() # 凡例の表示
# グラフの表示
plt.show()
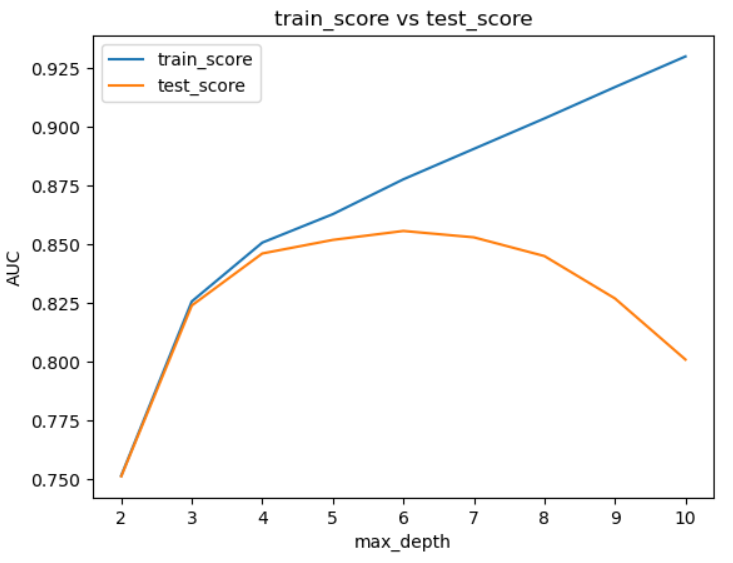
max_depth=6まではtestデータも改善しますが、それ以降は過学習になっている様子がよくわかります。
一応、bestなパラメーターを表示させてみますが、もちろんmax_depthは6になっています。
# 最適なパラメータの表示
print( gcv.best_params_ )
さて、それではこのベストパラメーターを使った場合のスコアを見てみます。
# 最適なパラメータで学習したモデルの取得
best_model = gcv.best_estimator_
# 評価用データの予測
pred_y3 = best_model.predict_proba(test_X)[:,1]
# AUCの計算
auc3 = roc_auc_score(test_y, pred_y3)
# AUCの表示
print ( auc3 )
約0.86と大きく改善しました!
さて、それでは改めてテストデータを提出してみます。
結果は以下の通りほぼ同様に改善しました。

目標であったチュートリアルの方のスコアを超えることができたのでこれで終わりでもいいのですが、せっかくなので簡単にいじれるところだけもう少し改善してみたいと思います。
上のグリッドサーチではmax_depthのパラメータしか探索しませんでしたが、他にもパラメータはあります。そこで、もう1つ効果がありそうなmin_samples_leaf(各葉が持つべき最小のサンプル数)も加えてみることにしました。
# 決定木モデルのインポート
from sklearn.tree import DecisionTreeClassifier as DT
# グリッドサーチのインポート
from sklearn.model_selection import GridSearchCV
# 決定木モデルの準備
tree = DT(random_state=0)
# パラメータの準備
parameters = {
'max_depth': [6, 8, 10, 12, 15, 20, 30],
'min_samples_leaf': [20, 25, 30, 35, 40, 45, 50, 55, 60]
}
# グリッドサーチの設定
gcv = GridSearchCV(tree, parameters, cv=5, scoring='roc_auc', return_train_score=True)
# グリッドサーチの実行
gcv.fit(train_X, train_y)ベストパラメータを表示させてみると以下の結果になりました。
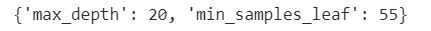
先ほどはmax_depth=6が最良だったのに、別のパラメータを加えると大幅に増えたのは意外でした。
その様子もグラフにしてみます。
import pandas as pd
import matplotlib.pyplot as plt
# cv_results_をDataFrameに変換
results = pd.DataFrame(gcv.cv_results_)
# グラフの設定
plt.title("Score vs min_samples_leaf for different max_depth")
plt.xlabel("min_samples_leaf")
plt.ylabel("Mean Test Score")
# max_depthの各値についてループ
for depth in parameters['max_depth']:
# max_depthが特定の値である結果だけを抽出
results_depth = results[results['param_max_depth'] == depth]
# max_depthが20の場合は点線でプロット
if depth == 20:
plt.plot(results_depth['param_min_samples_leaf'], results_depth['mean_test_score'], label=f'max_depth: {depth}')
else:
plt.plot(results_depth['param_min_samples_leaf'], results_depth['mean_test_score'], label=f'max_depth: {depth}', linestyle='dotted')
plt.legend(loc='upper left')
plt.show()
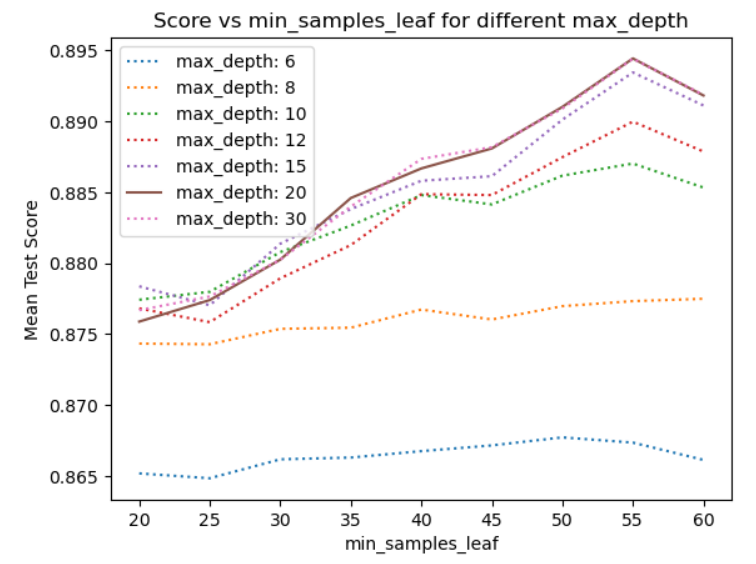
min_samples_leafを加えたことによって、先ほどのmax_depth=6よりも大きく改善することがわかります。この改善によって評価データのスコアは約89となり、提出用のテストデータもほぼ同程度まで改善しました。

アルゴリズムの変更による改善
もう十分満足できる数字ですが、もう1つだけ改善を加えてみます。それはモデルを変更することです。
これまで使用してきた決定木は主要な機械学習モデルの1つですが、これの応用版とでもいえる「ランダムフォレスト」や「勾配ブースティング」などのモデルはより精度の高いアウトプットが期待できます。
中でも勾配ブースティングモデルのLightGBMはコンペでも多様されているほど秀逸なモデルであるので、ここでもLightGBMを使用して、さらに代表的なパラメータについてグリッドサーチもかけてみます。
# LightGBMのインポート
import lightgbm as lgb
# グリッドサーチのインポート
from sklearn.model_selection import GridSearchCV
# LightGBMモデルの準備
lgbm = lgb.LGBMClassifier(random_state=0)
# パラメータの準備
parameters = {
'max_depth': [6, 8, 10, 12, 15, 20, 30],
'min_data_in_leaf': [20, 25, 30, 35, 40, 45, 50, 55, 60],
'num_leaves': [20, 30, 40, 50, 60]
}
# グリッドサーチの設定
gcv = GridSearchCV(lgbm, parameters, cv=5, scoring='roc_auc', return_train_score=True)
# グリッドサーチの実行
gcv.fit(train_X, train_y)
さきほどの決定木の内容が理解できていれば、コードの変更は難しくないですよね。
次にベストパラメーターを表示させつつ、スコアも算出してみます。
# 最適なパラメータの表示
print( gcv.best_params_ )
# 最適なパラメータで学習したモデルの取得
best_model = gcv.best_estimator_
# 評価用データの予測
pred_y3 = best_model.predict_proba(test_X)[:,1]
# AUCの計算
auc3 = roc_auc_score(test_y, pred_y3)
# AUCの表示
print ( auc3 )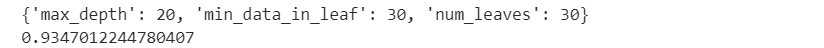
スコアが約0.93まで改善しました!
提出用のデータでも確認します。

こちらも0.93のスコアを獲得でき、少しの手間で大きく改善できました。
おわりに
この分析を通じてコンペ課題提出までの一連の作業は整理できましたし、またグリッドサーチの威力とモデル改善の効果を実感できました。
ここからさらに複数のモデルを組み合わせるなどまだまだ改善の余地はあるでしょうし、各特徴量についても最初に内容を確認したものの今回はまったく調整しておらず、こちらも削ったり組み合わせたりすることでよりよい成果が期待できそうです。
ただ、そのあたりは実コンペで試してみることにして、練習問題としてのこの課題の取り組みはここまでにします。
私の後にこの練習問題に取り組まれる方に、この記事を参考にしていただければ幸いです。





